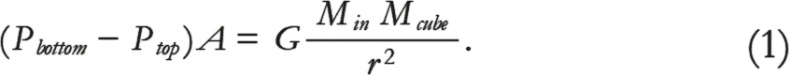Количество протонов в ядре мы обозначим буквой Z, для гелия Z = 2. Теперь можем выразить отношение между плотностью электронов n и массовой плотностью ρ:
и мы предположили, что масса протона, mp, равна массе нейтрона, что вполне достаточно для наших целей.
Величина mpA – это масса каждого ядра; тогда ρ / mpA – количество ядер на единицу объема, а Z – количество протонов на единицу объема, которое должно совпадать с количеством электронов, что и получается в уравнении.
Мы можем воспользоваться этим уравнением, чтобы заменить n в уравнении (3), и поскольку n пропорционально ρ, то оказывается, что давление варьируется пропорционально плотности в степени 5/3. Мы только что обнаружили существенную физическую закономерность:
и не стоит слишком беспокоиться по поводу конкретных цифр, задающих общий масштаб давления, так что мы просто объединили их всех в символе κ. Стоит отметить, что κ зависит от отношения Z и А, а потому будет отличаться для разных видов звезд – белых карликов. Объединение чисел в одном символе позволяет увидеть, что здесь важно. В нашем случае символы могут отвлечь от самого существенного, а именно от зависимости между давлением и плотностью звезды.
Прежде чем мы продолжим, нужно отметить, что давление, оказываемое квантовыми колебаниями, не зависит от температуры звезды. Важна только степень ее сжатия. Давление электронов будет несколько большим, потому что электроны «нормальным образом» перемещаются благодаря своей температуре, и чем жарче звезда, тем интенсивнее они перемещаются. Об этом источнике давления мы не стали говорить, потому что мало времени, а если бы пришлось его рассчитывать, мы бы выяснили, что он ничтожен по сравнению с гораздо большим квантовым давлением.
Итак, мы наконец-то можем вставить уравнение квантового давления в ключевое уравнение (1), которое стоит здесь повторить:
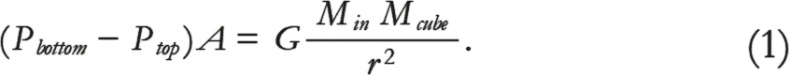
Однако все не так просто, как кажется, потому что нужно знать еще разницу давлений на верхнюю и нижнюю грани куба. Можно полностью переписать уравнение (1) относительно плотности внутри звезды, которая сама по себе меняется от места к месту внутри звезды (иначе бы вокруг куба не существовало никакой разницы давлений), а потом попытаться решить его, чтобы определить, как плотность изменяется с расстоянием от центра звезды. Но при этом придется решать дифференциальное уравнение, а математики такого уровня мы хотим избежать. Проявим изобретательность и предпочтем подольше подумать и поменьше посчитать, чтобы применить уравнение (1) для вывода взаимосвязи между массой и радиусом звезды – белого карлика.
Очевидно, что размер нашего кубика и его расположение внутри звезды совершенно произвольны, поэтому никакие выводы о самой звезде не могут зависеть от этих деталей. Начнем с того, что сделаем нечто совершенно бесполезное на первый взгляд.
Мы имеем возможность выразить размер и местонахождение нашего куба через размер всей звезды. Если R – радиус звезды, можно записать расстояние куба от центра звезды как r = aR, где a – просто безразмерное число между 0 и 1. Под безразмерностью мы понимаем то, что оно не соответствует никакой единице, это только численный показатель. Если a = 1, то куб находится на поверхности звезды, а если a = ½, куб расположен строго посередине. Точно так же можно выразить размер куба через радиус звезды. Если L – длина стороны куба, мы можем записать L = bR, где b – это опять же только численный показатель, который должен быть очень мал, если наш куб мал относительно звезды. Здесь нет абсолютно ничего сложного, так что на этом этапе все должно казаться настолько простым, что записывать, кажется, даже бесполезно.
Заметим только, что использовать расстояние R совершенно естественно, потому что нет других относящихся к белому карлику расстояний, которые могли бы представлять сколь-нибудь разумную альтернативу.
Мы можем продолжать свои «бессмысленные» занятия и выразить плотность звезды в месте нахождения куба через среднюю плотность звезды. Запишем, что ρ = fρ̅, где f – опять же просто численный показатель, а ρ̅ – средняя плотность звезды. Как мы уже указывали, плотность куба зависит от его положения внутри звезды – чем ближе к центру, тем больше плотность. Так как средняя плотность ρ̅ от положения куба не зависит, зависимость должен обнаруживать показатель f, который, таким образом, зависит от расстояния r, а следовательно, и от произведения aR. И это ключевая информация, лежащая в основе всех наших последующих вычислений: f – это чистое число, а R – не чистое число, а результат измерения расстояния. И f может зависеть только от a, а никак не от R. Это очень важный результат, потому что он свидетельствует, что плотность белого карлика «не зависит от масштаба». Это значит, что плотность изменяется на радиусе независимо от величины этого радиуса. Например, плотность в точке, расположенной на ¾ расстояния от центра до поверхности звезды, будет совершенно одинаковой в любом белом карлике независимо от его размера. Есть два способа оценки этого исключительно важного результата, и мы решили, что приведем здесь оба. Один из нас объясняет это так: «Дело в том, что любая безразмерная функция от r (а f – это именно она) может быть только безразмерной, так как это функция безразмерной переменной, а единственная безразмерная переменная в нашем случае – это r / R = a, поскольку R – единственная величина, связанная с расстоянием, из находящихся в нашем распоряжении».
Второй соавтор считает более четким следующее разъяснение: «f может в принципе по-разному сложным образом зависеть от r – расстояния кубика от центра звезды. Но давайте представим, что эти величины прямо пропорциональны, то есть f ∝ r. Иными словами, f = Br, где B – константа. Здесь самое важное то, что f – чисто численный показатель, в то время как r измеряется, например, в метрах. Отсюда следует, что B должно измеряться в 1/м, чтобы единицы расстояния взаимно сокращались. Итак, что нужно выбрать для B? Мы не можем назначить нечто произвольное, например «1 обратный метр», поскольку это бессмысленно и никак не связано со звездой. Почему, например, не выбрать один обратный световой год, получив совершенно другой ответ? Единственное расстояние, с которым мы имеем дело, – это R, физический радиус звезды, так что придется использовать его, чтобы f всегда оставалось чистым числом. Это значит, что f может зависеть только от r / R. Вы, наверное, уже поняли, что тот же вывод можно было сделать, если бы мы начали с предположения, что, например, f ∝ r²». Собственно, ровно то же говорил и первый соавтор, только сейчас вышло длиннее.