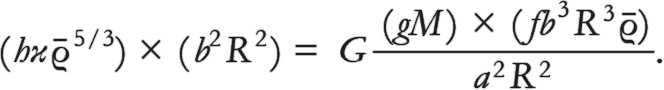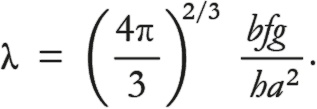Это значит, что можно выразить массу нашего кубика размером L и объемом L³, находящегося на расстоянии r от центра звезды, в виде Mcube = f(a)L³ρ̅. Мы написали f(a), а не просто f, чтобы не забывать, что f на деле зависит от нашего выбора a = r / R, а не от каких-то масштабных свойств звезды. Тот же аргумент можно использовать при указании, что мы можем записать Min = g(a)M, где g(a) – это опять же только функция от a. Например, функция g(a), высчитанная для a = ½, подсказывает, какое количество массы звезды приходится на сферу с радиусом, равным половине радиуса всей звезды, и это количество неизменно для всех белых карликов независимо от их радиуса по причине, приведенной в предыдущем абзаце
[61]. Вы могли заметить, что мы постоянно избавляемся от тех символов, которые встречаются в уравнении (1), заменяя их безразмерными величинами (a, b, f и g), помноженными на величины, зависящие только от массы и радиуса звезды (средняя плотность звезды определяется через M и R, поскольку ρ̅ = M / V и V = 4πR³ / 3, объем сферы). В довершение нужно сделать то же самое для разницы давлений, которую мы благодаря уравнению (4) можем записать как Pbottom – Ptop = = h(a, b)κρ̅5/3, где h(a, b) – безразмерная величина. То, что h(a, b) зависит одновременно от a и b, связано с тем, что разница давлений зависит не только от местоположения куба (представленного a), но и от его объема (представленного b): у более крупных кубов больше разница давлений. Самое важное здесь то, что, как и f(a), и g(a), h(a, b) не может зависеть от радиуса звезды.
Мы можем воспользоваться только что выведенными выражениями и переписать уравнение (1):
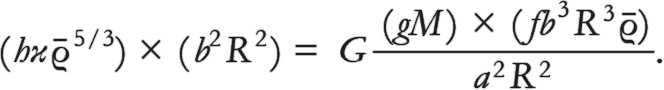
Кажется, что в уравнении царит хаос; непохоже, чтобы уже на следующей странице мы пришли к результату. Главное – заметить, что уравнение выражает отношения между массой звезды и ее радиусом – конкретная зависимость между ними уже нащупывается (или на виду, но чудовищно далека – в зависимости от вашего уровня владения математикой). После введения в наше хаотическое уравнение средней плотности звезды (то есть ρ̅ = M / (4πR³ / 3)) оно принимает следующий вид:

где
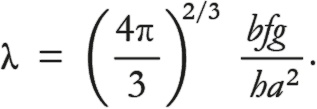
Теперь λ зависит только от безразмерных величин a, b, f, g и h, а следовательно, не зависит от величин, которые описывают звезду в целом, M и R, а следовательно, λ должна иметь одно и то же значение для всех белых карликов.
Если вас интересует, что произойдет, если изменить a и/или b (то есть изменить местоположение и/или размеры нашего кубика), то вы упустили главное в наших аргументах. Если понимать буквально, кажется, что изменение a и b изменит и λ, так что мы получим другой результат для RM⅓. Но ведь это невозможно, так как известно, что RM⅓ зависит от самой звезды, а не от конкретных свойств того кубика, который мы придумали (или не придумали).
Это значит, что любые изменения a или b должны компенсироваться соответствующими изменениями f, g и h.
Уравнение (5) довольно уверенно утверждает, что белые карлики могут существовать. Дело в том, что нам удалось уравновесить уравнение гравитации-давления – уравнение (1). Это было не так-то просто: вполне могло оказаться, что уравнению не удовлетворяет ни одно сочетание M и R. Уравнение (5) также предсказывает, что величина RM⅓ должна быть постоянной. Иными словами, если посмотреть на небо и измерить радиус и массу белых карликов, мы должны обнаружить, что радиус, помноженный на квадратный корень массы, даст один и тот же результат для любого белого карлика. Это смелое предсказание.
Только что изложенный аргумент можно еще усилить, поскольку возможно с точностью вычислить значение λ, правда, для этого придется решить дифференциальное уравнение второго порядка с учетом плотности, а такая математика лежит далеко за пределами нашей книги. Помните, что λ – это чистое число: оно значит только «то, что значит», и мы можем вычислить его с привлечением математики чуть более высокого уровня. Тот факт, что здесь мы не стали этим заниматься, не должен затмевать наших достижений: мы доказали, что белые карлики могут существовать, и сумели сделать предсказание, связанное с их массой и радиусом. После вычисления λ (которое можно выполнить на домашнем компьютере) и введения значений для κ и G наше предсказание примет вид:
RM⅓ = (3,5 × 1017 кг⅓ м) × (Z / A)5/3,
что равняется 1,1 × 1017 кг1/3 м для ядер, состоящих из чистого гелия, углерода или кислорода (где Z / A = ½). Для железных ядер Z / A = 26/56, так что 1,1 сводится почти к 1,0. Мы пролистали справочную литературу и собрали данные о массах и радиусах 16 белых карликов, расположенных в Млечном Пути, ближайшей к нам галактике. Для каждой такой звезды мы вычислили значение RM⅓, и результаты астрономических наблюдений показали, что оно приблизительно равно 0,9 × 1017 кг⅓ м. Соответствие между наблюдениями и теоретическими выкладками просто поразительное: с помощью принципа Паули, принципа неопределенности Гейзенберга и закона притяжения Ньютона мы сумели предсказать зависимость между массой и радиусом для белых карликов.
Разумеется, в числах есть некая приблизительность (например, теория дает 1,1 или 1,0, а результат наблюдений – 0,9). Будь у нас настоящий научный анализ, мы бы начали сейчас говорить, насколько вероятно полное соответствие теории эксперименту, но для наших целей такой аналитический уровень не столь необходим, потому что соответствие и так удивительно неплохое. Просто фантастика, что мы сумели подсчитать все это с погрешностью примерно 10 %, и это убедительное доказательство нашего приличного понимания квантовой механики и звезд.