Представьте снова садовый шланг, который можно рассматривать как длинный резиновый лист, свернутый в трубку малого поперечного сечения. На этот раз мы полагаем, что шланг — это вся вселенная (а не объект внутри вселенной)
[21]. Если бы вселенная имела форму такого садового шланга, у нас было бы одно очень длинное измерение и одно очень маленькое, свернутое измерение. Это именно то, что мы хотим.
Для небольшого существа, например, плоского жука, живущего во вселенной садового шланга, она выглядела бы двумерной. (В таком сценарии наш жук должен быть приклеен к поверхности шланга — двумерная вселенная не включает внутренность шланга, которая трехмерна.) Жук может ползать в двух направлениях: вдоль шланга или вокруг него. Как Додо, который мог бегать по кругу в своей двумерной вселенной, жук, начавший движение из какой-то точки на шланге, может проползти вокруг него и в конце концов вернуться к тому месту, с которого начал. Так как второе измерение мало, жуку не придется слишком далеко уползать, чтобы вернуться.
Если популяция живущих на шланге жуков испытывает воздействие сил, например, электрических или гравитационных, эти силы способны притягивать или отталкивать жуков в любом направлении по поверхности шланга. Жуки могут быть отделены друг от друга либо вдоль длины шланга, либо по его окружности, и могут испытывать действие любой силы, присутствующей на шланге. Если разрешение достаточно для того, чтобы различать столь малые расстояния, как диаметр шланга, силы и тела проявляют оба измерения, которые и есть на самом деле.
Однако, если бы наш жук мог обозреть окружающее его пространство, он бы заметил, что два измерения очень различны. Одно измерение, вдоль длины шланга, очень большое. Он может быть даже бесконечно большим. В то же время другое измерение очень мало. Два жука никогда не расползутся очень далеко друг от друга в направлении вокруг шланга. И жук, пытающийся совершить далекое путешествие в этом направлении, очень скоро попадет туда, откуда он начал свой путь. Сообразительный жук, любящий тренировать свои ноги, знал бы, что его вселенная двумерна, и что одно измерение тянется далеко-далеко, а другое очень мало и свернуто в окружность.
Однако точка зрения жука совершенно отлична от точки зрения, которую имели бы существа вроде нас во вселенной Клейна, в которой дополнительное измерение свернуто до чрезвычайно малого размера, равного 10-33 см. В отличие от жука мы никогда не станем достаточно маленькими, чтобы обнаружить или прогуляться по измерению столь малого размера.
Итак, чтобы завершить нашу аналогию, предположим, что во вселенной садового шланга живет существо, значительно большее, чем жук, обладающее только грубым разрешением и поэтому не способное детектировать малые тела или структуры. Так как линза, через которую большое существо наблюдает за миром, смазывает все детали, столь же малые как диаметр шланга, то с точки зрения этого существа дополнительное измерение будет невидимым. Существо будет видеть только одно измерение. Понять, что вселенная садового шланга имеет более одного измерения, можно, только если обладать зрением столь острым, чтобы различить нечто столь малое, как ширина шланга. Но если зрение не такое острое, чтобы различить эту ширину, существо всегда будет видеть только линию.
Кроме того, физические явления не выдадут существования дополнительного измерения. Большие существа во вселенной садового шланга заткнут второе, маленькое измерение и никогда не узнают, что оно здесь было. Не имея возможности обнаружить структуру или изменения вдоль дополнительного измерения типа раскачки или волн материи или энергии, они никогда не зарегистрируют его существование. Любые изменения вдоль второго измерения будут полностью смыты, подобно тому как вы никогда не заметите какое-либо изменение толщины листа бумаги в масштабе его атомной структуры.
Двумерный мир, в котором оказалась во сне Афина, был очень похож на вселенную садового шланга. Так как у Афины были возможности становиться как большой, так и малой относительно ширины 2D-ленда, она могла наблюдать эту вселенную как с точки зрения кого-то большего по размерам, по сравнению со вторым измерением этой вселенной, так и с точки зрения кого-то меньшего по размерам. Для большой Афины 2D-ленд и 1D-ленд выглядели полностью одинаковыми. Только маленькая Афина могла указать на различие. Так и во вселенной садового шланга существо будет находиться в полном неведении относительно дополнительного пространственного измерения, если не станет достаточно маленьким, чтобы его увидеть.
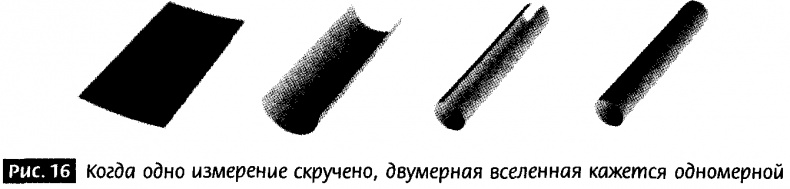
Вернемся к вселенной Калуцы — Клейна, у которой есть три известных нам пространственных измерения и дополнительное невидимое измерение. Чтобы обдумать ситуацию, можно опять использовать рис. 16. В идеале, мне следовало бы нарисовать четыре пространственных измерения, но, к сожалению, это невозможно (не поможет даже книжка-раскладушка с объемными разворотами). Однако, поскольку три бесконечных измерения, образующих наше пространство, качественно одинаковы, мне нужно реально нарисовать только одно типичное измерение. Это позволяет мне использовать другое измерение, чтобы представить невидимое дополнительное измерение. Показанное здесь другое измерение свернуто и этим оно фундаментально отличается от трех других.
Точно так же как в примере с двумерной вселенной садового шланга, четырехмерная вселенная Калуцы — Клейна с одним крохотным свернутым измерением будет казаться нам имеющей на одно измерение меньше, чем те четыре, которые есть на самом деле. Так как мы ничего не можем знать о дополнительном пространственном измерении, пока не сумеем получить свидетельство о его структуре в крохотном масштабе этого измерения, вселенная Калуцы — Клейна будет казаться трехмерной. Свернутые или компактифицированные дополнительные измерения никогда не будут обнаружены, если их масштабы достаточно малы. Позднее мы исследуем вопрос, насколько они должны быть малы, однако сейчас достаточно понимать, что планковская длина находится далеко за порогом измеримости.
В жизни и в физике мы регистрируем только те детали, которые действительно для нас важны. Если вы не можете наблюдать детальную структуру, вы можете с тем же успехом считать, что ее нет. В физике это пренебрежение локальными деталями реализуется в идее эффективной теории, о чем шла речь в предыдущей главе. Все, что имеет значение в эффективной теории, — это вещи, которые вы можете реально воспринимать. В приведенном выше примере мы будем использовать трехмерную эффективную теорию, в которой подавлена информация о дополнительных измерениях.



