Как и ранее, можно вообразить фиксированное число силовых линий, идущих от массивного шара. На расстояниях, меньших размеров дополнительных измерений, эти силовые линии распространяются равномерно во всех направлениях. Если бы вы могли измерить тяготение на этом малом масштабе, вы бы получили следствия многомерной гравитации. Силовые линии распространялись бы так же, как вода, поступающая в шланг через прокол и распределяющаяся по внутренней части шланга.

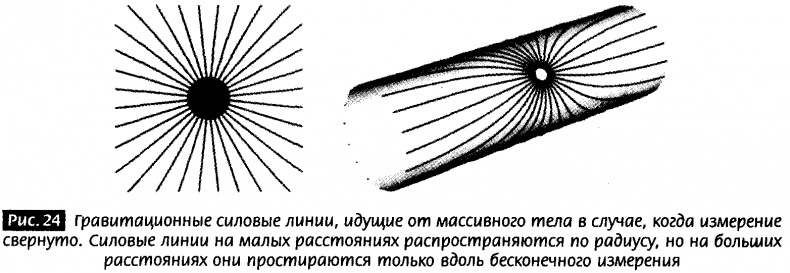
Однако на расстояниях больших, чем размеры дополнительных измерений, силовые линии могут распространяться только по бесконечным направлениям (рис. 24). В малых компактных измерениях силовые линии наткнутся на край пространства, так что они не смогут распространяться по этому пути дальше. Они должны искривиться, и единственный оставшийся для них путь — двигаться в направлении больших измерений. Поэтому на расстояниях, больших, чем размеры дополнительных измерений, все выглядит так, как будто дополнительных измерений нет, и закон силы превращается в ньютоновский закон обратных квадратов, который мы и наблюдаем. Это означает, что даже с качественной точки зрения вы не можете знать о существовании дополнительных измерений, если измеряете гравитационную силу только между телами, расстояние между которыми больше размера свернутого измерения. Зависимость от расстояния отражает существование дополнительных измерений только в крохотной области внутри компактного пространства.
О других способах ограничить измерения
Теперь мы установили, что когда дополнительные измерения достаточно малы, они невидимы, и отсутствуют какие-либо измеримые следствия их существования в масштабах длин, которые мы наблюдаем. В течение долгого времени теоретики-струнники предполагали, что дополнительные измерения — это измерения, имеющие планковскую длину, однако недавно некоторые из нас поставили это предположение под вопрос.
Никто не понимает теорию струн настолько хорошо, чтобы с определенностью сказать, какие размеры окажутся у дополнительных измерений. Возможны размеры, сравнимые с планковской длиной, но и любое измерение, слишком маленькое для того, чтобы его можно было увидеть, тоже допустимо. Планковская длина настолько мала, что даже значительно большие Свернутые измерения могут ускользнуть от наблюдения. Важный вопрос при изучении дополнительных измерений состоит в том, насколько велики могут быть эти измерения, если допустить, что мы их до сих пор не видели.
Среди вопросов, обсуждаемых в этой книге, есть и вопросы о том, насколько велики могут быть дополнительные измерения, приводят ли эти измерения к каким-либо заметным явлениям в мире элементарных частиц и как это можно экспериментально исследовать. Мы увидим, что существование дополнительных измерений может существенно изменить правила, по которым мы изучаем физику частиц, и, более того, некоторые из этих изменений могут привести к экспериментально наблюдаемым следствиям.
Еще более радикальный вопрос, который мы исследуем, состоит в том, должны ли дополнительные измерения быть малыми. Мы не видим крохотных измерений, но обязаны ли измерения быть маленькими для того, чтобы быть невидимыми? Может ли дополнительное измерение простираться бесконечно, но так, чтобы мы его не видели? Если такое возможно, то дополнительные измерения будут сильно отличаться от тех измерений, которые мы рассматривали. Пока что я нашла только простейшую возможность. Позднее мы увидим, почему даже такое радикальное предположение о бесконечном дополнительном измерении не может быть исключено, если оно существенно отличается от трех привычных нам бесконечных измерений.
В следующей главе будет рассмотрен еще один вопрос, который мог у вас возникнуть: почему малые дополнительные измерения не могут быть просто отрезками, не свернутыми в шарик, а просто ограниченными двумя «стенками»? Такая возможность не приходит в голову сразу, но почему нет? Ответ состоит в том, что идея о конце пространства подразумевает знание того, что там происходит. Испытывает ли все на краю вселенной резкий обрыв, как, по-видимому, следует из старых картин плоской Земли? Или все отражается обратно? Или туда никогда нельзя попасть? Необходимость уточнения того, что происходит на краю, означает, что вы должны знать то, что ученые называют граничными условиями. Если пространство кончается, то где это происходит и на чем все кончается?
Браны — мембраноподобные объекты в многомерном пространстве — обеспечивают необходимые граничные условия для миров, которые «кончаются». Как мы увидим в следующей главе, браны могут сделать мир (или много миров) разнообразными.
Глава 3
Исключительные пассажи: браны, миры на бранах и балк
I’m gonna stick like glue,
Stick, because I’m stuck on you.
Elvis Presley
[23]
В противоположность трудолюбивой Афине, Икар редко читал книги. Чаще всего он предпочитал компьютерные игры и возню со всякими техническими приспособлениями и автомобилями. Но Икар не выносил ездить в Бостон, где водители были неосторожны, дороги плохо размечены, а все шоссе непрерывно находились в состоянии ремонта, каждая поездка Икара заканчивалась тем, что он застревал в пробке, что особенно его расстраивало, когда он видел над головой свободную дорогу по воздуху. Она манила Икара, но у него не было возможности быстро до нее добраться, так как не в пример совам Афины он не мог летать. Для Икара, застрявшего в бостонских пробках, третье измерение было вообще ни к чему.
Еще совсем недавно очень мало уважающих себя физиков считали, что дополнительные измерения заслуживают того, чтобы об них думать. Эти измерения были слишком умозрительны и слишком незнакомы — никто не мог сказать о них что-то определенное. Однако в последние годы судьба улыбнулась дополнительным измерениям. Их перестали избегать, как нежелательных незваных гостей, они превратились в очень популярную, стимулирующую размышления деятельность. Вновь обретенная респектабельность обязана своим происхождением бранам и тем поистине новым теоретическим возможностям, которые возникли благодаря этим поразительным конструкциям.
Браны ворвались в физическое сообщество, как ураган, в 1995 году, когда физик Джо Полчинский из Института теоретической физики Кавли в Санта-Барбаре установил, что они важны для теории струн. Но даже до этого физики предлагали браноподобные объекты. Одним таким примером была р-брана, объект, который простирается бесконечно далеко только в нескольких измерениях и который был математически выведен физиками с помощью эйнштейновской общей теории относительности. Физики, занимающиеся частицами, также предлагали механизмы удержания частиц на браноподобных поверхностях
[24]. Однако браны в теории струн были первым известным типом бран, который может удерживать не только частицы, но и силы, и вскоре мы увидим, что это — часть тех свойств, которые делают браны столь интересными. Как Икар, застрявший на двумерной дороге в трехмерном пространстве, частицы и силы могут быть захвачены на поверхностях меньшего числа измерений, называемых бранами, даже если у вселенной есть еще много других измерений. Если теория струн правильно описывает мир, в котором мы живем, у физиков не остается иного выбора кроме признания потенциальной возможности существования таких бран.




