Разовьем это понятие чуть дальше. Икар Рашмор III (из рассказанной выше истории), житель Бостона, — характер посложнее. На самом деле, он трехмерен. Икару двадцать один год, он водит спортивные автомобили и проигрывает деньги в Вандерленде, городе вблизи Бостона, где есть трек для собачьих бегов. На рис. 4 я изобразила Икара. Хотя он и нарисован на двумерной поверхности куска бумаги, наличие трех осей говорит о том, что Икар, безусловно, трехмерен
[7].
Однако, описывая большинство людей, мы обычно присваиваем им более одной или даже более трех характеристик. Афине, сестре Икара, одиннадцать лет, она жадно поглощает книги, отличается математическими способностями, интересуется текущими событиями и заботится о маленьких совятах. Вы можете захотеть изобразить все это на графике (хотя зачем это вам, я не очень понимаю). В этом случае Афина будет изображаться точкой в пятимерном пространстве, оси которого соответствуют возрасту, числу прочитанных за неделю книг, среднему числу баллов за тесты по математике, числу минут в день, затрачиваемых на чтение газет, и числу имеющихся в доме совят. Однако нарисовать такой график затруднительно. Для этого потребуется пятимерное пространство, которое очень трудно изобразить. Даже компьютерные программы поддерживают только 3D-графику.
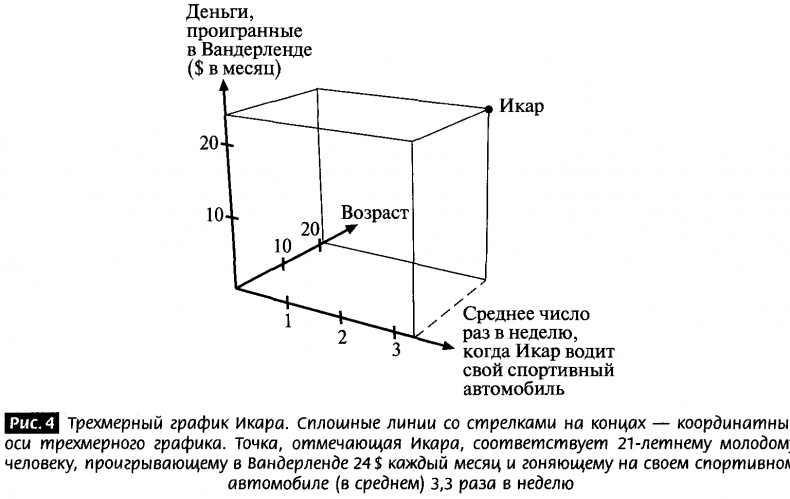
Тем не менее, в абстрактном смысле, существует пятимерное пространство и набор пяти чисел, например (11, 3, 100, 45, 4), говорящих нам, что Афине 11 лет, она в среднем читает 3 книги каждую неделю, всегда отвечает правильно на математические вопросы, тратит каждый день 45 минут на чтение газет и в данный момент в доме живет 4 совы. Этими пятью числами я описала Афину. Если бы вы ее знали, вы могли бы опознать ее по точке в пяти измерениях.
Число измерений для каждого из трех описанных выше людей — это число признаков, использованных мной для их идентификации: один для Сэма, три для Икара и пять для Афины. Конечно, реальных людей в общем случае трудно описать таким небольшим числом единиц информации.
В последующих главах мы будем использовать измерения для описания не людей, а самого пространства. Под «пространством» я понимаю область, в которой существует материя и происходят физические явления. Пространство определенного числа измерений — это-пространство, требующее для задания любой его точки определенного числа величин. В одном измерении это будет точка на графике с единственной осью x; в двух измерениях — точка на графике с осями х и у, в трех измерениях — точка на графике с осями х, у и z
[8]. Эти оси показаны на рис. 5.
Все, что нужно для знания вашего точного положения в трехмерном пространстве — это три числа. Задаваемые числа могут быть долготой, широтой и высотой, или длиной, шириной и высотой. Вы можете иным способом выбрать ваши три числа. Решающим является то, что наличие трех измерений означает, что вам требуется ровно три числа. В двумерном пространстве вам требуется два числа, а в пространствах с большим числом измерений вам нужно больше чисел.
Когда число измерений больше, это означает, что вы свободно можете двигаться по большему числу совершенно различных направлений. Точка в четырехмерном пространстве просто требует одну дополнительную ось, которую трудно нарисовать. Но совершенно нетрудно вообразить ее существование. Мы размышляем об этом, используя слова и математические термины.
В теории струн требуется еще больше измерений: эта теория постулирует существование шести или семи дополнительных координат, для того чтобы изобразить точку. Совсем недавние работы по теории струн показали, что число измерений может быть даже еще больше. В этой книге я буду придерживаться открытой точки зрения и допущу возможность существования любого числа дополнительных измерений. Рано говорить, сколько измерений имеет Вселенная на самом деле. Многие представления о дополнительных измерениях, которые я буду описывать, применимы к любому числу дополнительных измерений. В тех редких случаях, когда это будет не так, я об этом скажу специально.
Однако описание физического пространства включает больше, чем простую идентификацию точек. Вам нужно также задать метрику, которая устанавливает масштаб измерений или физическое расстояние между двумя точками. Это соответствует меткам вдоль оси графика. Недостаточно знать, что расстояние между парой точек равно 17, пока вы не знаете, означает ли 17 на самом деле 17 сантиметров, 17 миль или 17 световых лет. Метрика требуется для того, чтобы объяснить, как измерять расстояние, и установить, какому расстоянию в описываемом нами с помощью графика мире соответствует расстояние между двумя точками на этом графике. Метрика дает измерительную линейку, которая определяет ваш выбор единиц, с тем чтобы установить масштаб, аналогично тому, как это делается на карте, когда полдюйма может соответствовать одной миле, или в метрической системе, которая задает метровый эталон, с которым мы все соглашаемся.
Но метрика определяет не только это. Она также говорит нам, изгибается ли, закручивается ли пространство, как поверхность воздушного шара, когда он при надувании превращается в сферу. Метрика содержит всю информацию о форме пространства. Метрика кривого пространства говорит как о расстояниях, так и об углах. Точно так же как сантиметр может соответствовать разным расстояниям, угол может описывать разные формы. Я подробнее расскажу об этом позднее, когда мы будем анализировать связь между кривым пространством и тяготением. Пока что скажем просто, что поверхность шара — совсем не то же самое, что и поверхность плоского листа бумаги. Треугольники на одной поверхности выглядят иначе, чем на другой, и разницу между этими двумерными пространствами можно увидеть в их метрике.
В процессе развития физики менялось и количество информации, спрятанной в метрике. Когда Эйнштейн развивал теорию относительности, он заметил, что четвертое измерение — время — неотделимо от трех измерений пространства. Время тоже нуждается в масштабе, так что Эйнштейн описал гравитацию с помощью метрики четырехмерного пространства-времени, добавив временное измерение к трем пространственным измерениям.
Дальнейшие исследования показали, что могут существовать дополнительные пространственные измерения. В этом случае истинная метрика пространства-времени будет включать более трех измерений пространства. Число измерений и метрика таких измерений определяет то, как мы описываем такое многомерное пространство. Но прежде чем мы исследуем нашу метрику и метрику многомерных пространств подробнее, подумаем еще немного о смысле термина «многомерное пространство».




