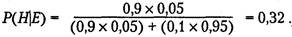
Так, согласно этой модели, шансы нежелательной встречи на вечеринке составляют примерно 1/3. При таком раскладе вы можете принять научно обоснованное решение о том, насколько тягостной может оказаться эта встреча и насколько приятной будет вечеринка. Пожалуй, вам стоит позвонить пригласившему вас другу.
Однако насколько хорошо теорема Байеса согласуется с реальной жизнью? Весьма маловероятно, что, находясь в вышеописанных обстоятельствах, вы достали бы из кармана калькулятор и начали вычислять величину Р(Н|Е). Некоторые данные, собранные Эдвардсом (Edwards, 1968), указывают на то, что мы оцениваем обстоятельства условной вероятности более консервативно, чем это предполагает теорема Байеса. Изучая влияние новой информации на оценки испытуемых, Эдвардc давал студентам колледжа два мешка по 100 покерных фишек в каждом. В одном мешке было 70 красных фишек и 30 синих, а в другом — 30 красных и 70 синих. Наугад выбирался один из мешков, и испытуемые должны были определить, который это мешок из двух, вынимая из него по одной фишке, рассматривая ее и возвращая обратно в мешок, а затем продолжая процесс. Первоначально вероятность вынуть красную фишку из мешка, где больше красных фишек, составляет 70%, а из мешка, где больше синих, — 30%. Однако если мы вынули из мешка только одну фишку и она оказалась красной, тогда, согласно теореме Байеса, вероятность того, что в этом мешке доминируют красные, равна 70%. Люди обычно недооценивают реальное (математическое) значение этого наблюдения и предполагают, что вероятность того, что в этом мешке доминируют красные, равна 60%. Если следующая фишка тоже красная, то реальная вероятность того, что это «красный» мешок, равна 84%. Суждения испытуемых в этом случае, как и при более крупных выборках, остаются консервативными.
Проделка Фидо
Предположим, что вы оставили вашу собаку по кличке Фидо охранять ваш дом от грабителей, которые могут ворваться и украсть 10-фунтовый кусок мяса, размораживающийся на столе. Когда вы вернулись, все замки были в порядке, так что вы уверены, что никаких грабителей здесь не было. Однако мясо пропало. Само собой разумеется, что главный подозреваемый — Фидо.

На основе прошлого опыта, двух визитов к собачьему психиатру и хитрого взгляда вы оцениваете вероятность того, что это сделал Фидо, как 0,95. Однако, прежде чем обвинить Фидо, вы решаете получить еще одну улику. Вы готовите его обычный обед и предлагаете ему. К вашему удивлению, он съедает его до последней крошки. Едва ли этого можно ожидать от вора, который только что съел 10 фунтов мяса. Вы оцениваете вероятность того, что Фидо может сделать это, если он действительно съел мясо лишь в 0,02. Хотя обычно у него хороший аппетит и он съедает свой обед с вероятностью 0,99. Как вы должны пересмотреть ваши первоначальные подозрения, учитывая охотно съеденный обед? Очевидно, может оказаться полезной теорема Байеса. Учитывая только что съеденный обед, вероятность того, что Фидо виновен, можно выразить следующим образом:

До эксперимента с обедом обстоятельства складывались не в пользу Фидо. Однако при помощи теоремы Байеса мы смогли учесть результаты эксперимента с обедом и заключить, что Фидо, скорее всего, невиновен. Всякий любитель собак может на этом примере увидеть полезность теоремы Байеса.
Применение теоремы Байеса к задачам «реального мира» — это особый вопрос, поскольку трудно точно оценить вероятность событий. Рассмотрим пример из международной политики. Несколько лет назад в отношениях между бывшим СССР и США существовала значительная напряженность, что, по мнению многих людей, привело к увеличению вероятности возникновения открытой агрессии, а может, и тотальной войны. Если бы можно было точно оценить все силы и определить вероятность начала войны, то в формулу Байеса можно было бы включить влияние событий, определяющих вероятность мира или войны (таких, как встреча бывших президентов Клинтона и Ельцина), и, что особенно ценно, можно было бы получить вероятностную статистику. Некоторые честолюбивые ученые, работающие в области психологии, социологии и политологии, как раз и предприняли именно такие глобальные исследования.
За последние несколько лет интерес к байесовским методам возрос (Malakoff, 1999). Одна из причин увеличения количества статей на эту тему — повсеместное распространение персональных компьютеров и развитие новых алгоритмов. Некоторые использовали методы моделирования, известные как цепи Маркова и метод Монте-Карло (знакомые посвященным по аббревиатуре МСМС — Markov Chain Monte Carlo), в которых применяются байесовские методы, чтобы использовать имеющиеся знания для предсказания самых разных событий, от ядерного магнитного резонанса до вероятного подозреваемого в совершении преступления. Последний вариант использования был признан сомнительным вследствие «расового профилирования».
Принятие решений и рациональность
Может показаться, что homo sapiens изначально изображается в этой главе как самое рациональное из существ. Так, наше обсуждение процесса формирования понятий в конце концов показало, что все нормальные существа формируют понятия при помощи рациональных правил. При обсуждении формального мышления мы узнали, что достоверность аргументации можно определить на основе законов логики, несмотря на то что люди склонны обманываться как структурой аргументации, так и ложным содержанием. Наконец, в предыдущем разделе, посвященном принятию решений, мы узнали, что «рациональный» человек обычно становится нерациональным, когда дело касается принятия решений о нескольких событиях.
Я думаю, было бы глупо утверждать, что все люди столь же рациональны, как вы или я (или какими мы себя представляем), но являемся ли мы как вид настолько нерациональными, как это может показаться, если исходить из эмпирических результатов, собранных на материале задач по принятию решений?
При тщательном изучении результаты Тверски и Канемана, а также результаты изучения формального мышления заставляют предположить, что люди не являются абсолютно рациональными созданиями. Некоторые пытаются опровергнуть эти результаты, критикуя построение экспериментов и неизбежно следующие из них философские выводы. Коуэн (Cohen, 1981) из Оксфордского университета — один из таких критиков; он утверждает, что: 1) рациональность должна определяться в процессе наблюдения за обычными людьми, а не в ходе хитрых лабораторных экспериментов, которые построены не так, чтобы реально иллюстрировать повседневное принятие решений, и плохо соответствуют реальной ситуации; 2) совершенно неразумно ожидать от обычных людей умудренности в законах вероятности и статистики, которыми во многих экспериментах описываются базисная линия и отклонения от нее; 3) законы логики и рациональности не определяют поведения обычного человека. Вспомним того несчастного, который пытался избежать встречи со своей бывшей любовью. Используя теорему Байеса, вероятность этой встречи, если девушка действительно пошла на вечеринку, составляла 0,32. Как бы повлияло это число на поведение того человека? Если взаимная неприязнь у этой пары велика («Да я на сотню миль не подойду к ней»), эта цифра бессмысленна для предсказания поведения.

