У большинства появляется версия (которую разделяют и опрошенные Амосом медицинские специалисты), что нужно принять синюю таблетку, потому что: а) у них синее лицо; и б) цвет их лица соответствует большинству случаев – 75 %. Но при этом игнорируются базовые показатели заболевания.
Заполняем четырехпольную таблицу. У нас нет данных о количестве населения, с которым мы имеем дело, поэтому, чтобы облегчить задачу с таблицей, предположим, что всего населения 120 человек
[590] (это число вы видите в нижней правой колонке вне таблицы). Из условий задачи мы знаем достаточно информации, чтобы заполнить остальную часть таблицы.
Поскольку «зеленая» болезнь встречается в 5 раз чаще, чем «синяя», это означает, что из 120 человек, имеющих то или иное заболевание, у 100 должно быть «зеленое» лицо, а у 20 – «синее»
[591].
Поскольку ваш цвет лица соответствует 75 % случаев заболевания, у 75 % людей с синим лицом наличествует «синяя» болезнь. 75 % от 20 = 15. Остальная часть таблицы заполняется по тому же принципу.
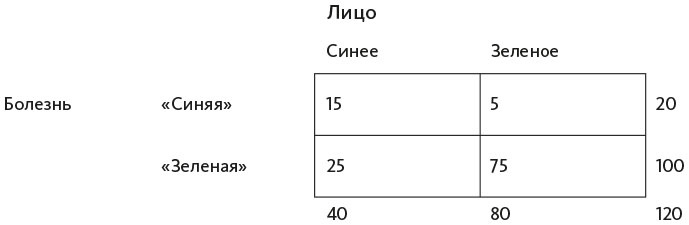
Теперь, прежде чем принять синюю таблетку – которая либо вылечит вас, либо убьет, – задайте себе байесовский вопрос: «Какова вероятность того, что у меня “синяя” болезнь, учитывая, что лицо синее?» Ответ: из 40 человек с лицом такого цвета «синей» болезнью страдают 15; 15: 40 = 38 %. Вероятность того, что у вас «зеленая» болезнь при наличии синего лица, 25 из 40, или 62 %. Для вас вернее принять зеленую таблетку независимо от того, какого цвета ваше лицо, потому что заболевание, признаком которого является зеленое лицо, встречается гораздо чаще, чем «синяя» болезнь. Опять же, мы противопоставляем базовые показатели симптомам и знаем, что их не следует игнорировать. Это трудно сделать в уме, но четырехпольная таблица позволяет так визуально организовать информацию, что ее легче воспринимать. Подобные расчеты дадут ответ на вопрос, почему врачи часто, еще до того, как получают результаты анализов пациента, проясняющих, что не так, начинают лечение с антибиотиков. Дело в том, что некоторые антибиотики работают против широкого спектра заболеваний, поэтому их и назначают сразу.
В примере с блуритом, с которого я начал, положительные анализы были у 201 человека, из которых болел только один. Во многих реальных случаях в системе здравоохранения всем этим людям будут давать лекарства. Это иллюстрирует еще одно важное понятие в медицинской практике – количество нуждающихся в лечении. Таким термином обозначают число людей, которые должны пройти лечение, например медикаментозное или хирургическое, прежде чем один человек выздоровеет. Число 201 для тех, кому нужна врачебная помощь, не необычно для современной медицины. Есть некоторые регулярно выполняемые операции, где число нуждающихся в лечении составляет 48 пациентов, а для некоторых препаратов это число может превышать 300. Если оставить в стороне синее лицо и анализы на воображаемые болезни, что можно сказать о решениях, от которых действительно зависит чья-то жизнь? Врач говорит, что эти лекарства в 40 % случаев позволят прожить еще пять лет. Как вы оцениваете этот шанс?
Есть способ подойти к этому решению с той же ясной рациональностью, которую мы применили к задачке при выборе двух ядов, используя концепцию «ожидаемой выгоды». «Ожидаемая выгода» от чего-то – это вероятность этого события, умноженная на выгоду, получаемую в результате. Руководители предприятий регулярно оценивают финансовые решения с помощью этого метода. Предположим, на вечеринке кто-то подходит к вам и предлагает сыграть: он будет подбрасывать обычную монету, и вы получите один доллар каждый раз, когда выпадет решка. Сколько бы вы заплатили, чтобы сыграть? (Предположим, что сейчас вам не очень нравится игра, хотя вы и не против; гораздо сильнее интересует возможность заработать.) Ожидаемая выгода составляет 50 центов, то есть вероятность выпадения решки (0,5), умноженная на выигрыш (один доллар). Обратите внимание, что ожидаемая выгода зачастую оказывается не той суммой, которую вы можете выиграть: здесь вы либо ничего не получаете, либо получаете один доллар. Но за многие сотни повторений должны заработать около 50 центов за игру. Если вы платите менее 50 центов за игру, в долгосрочной перспективе вы останетесь в выигрыше.
Понятие ожидаемой выгоды можно применить и к убыткам. Предположим, вы сомневаетесь, платить ли за парковку в центре города или пристроиться в зоне погрузки, рискуя нарваться на штраф. Представьте, что парковка стоит 20 долларов, а штраф за неправильную парковку – 50 долларов. Вы знаете: вероятность, что вас оштрафуют, только 25 %. Тогда ожидаемая выгода от парковки составляет –20 долларов: у вас есть стопроцентный шанс заплатить 20 долларов (я написал с минусом, чтобы указать на потерю).
Решение выглядит следующим образом:
1. Оплата парковки: стопроцентный шанс потерять 20 долларов.
2. Не платить за парковку: двадцатипятипроцентный шанс потерять 50 долларов.
Ожидаемая выгода от получения штрафа за парковку составляет 25 % × (–50 долларов), получаем –12,50 доллара. Теперь, конечно, вы ненавидите штрафы и хотите обойтись без них. Допустим, вам сегодня не везет, и вы не хотите рисковать. И поэтому можете заплатить 20 долларов за парковку, чтобы избежать вероятности штрафа 50 долларов. Однако рациональный способ оценить это решение – посмотреть на него в долгосрочной перспективе. Мы сталкиваемся с сотнями подобных выборов в повседневной жизни. И действительно важно то, что получится в среднем. Ожидаемая выгода для этого конкретного варианта заключается в том, что вы выйдете вперед в долгосрочной перспективе, заплатив штрафы
[592]: потеря в среднем 12,50 доллара по сравнению с потерей 20 долларов. За год стоянки раз в неделю на этой улице вы будете тратить 650 долларов, а не 1040 долларов на парковках
[593], – это большая разница. Конечно, каждый день можно применять байесовскую корректировку. Если вы видите, что к вашей машине, поставленной в зоне погрузки, приближается охранник стоянки, чтобы выписать штраф, то сегодня правильный день для переезда на парковку.




