Идея, которая сейчас может казаться простой, для того времени была абсолютно контринтуитивна. Она состоит в том, что на основе данных о поведении некой группы людей в прошлом мы можем сделать статистические выводы о том, что случится с этой или другой похожей группой в будущем.
Вот как выглядит расчет выбора правильного решения во время эпидемии оспы в Бостоне начала XVIII века.
В 1721 году население Бостона составляло 10700 человек.
Инокуляцию сделали 286 бостонцев. Из них остались в живых 280, а 6 человек погибло.
5759 жителей не сделали инокуляцию и заболели естественным путем. 4915 из них выжили, 844 погибли.
4655 человека не заболели оспой, и, соответственно, все они остались живы. Если бы все они согласились на процедуру, кто-то из них бы погиб.
Проще всего представить последствия инокуляции в виде такого дерева.
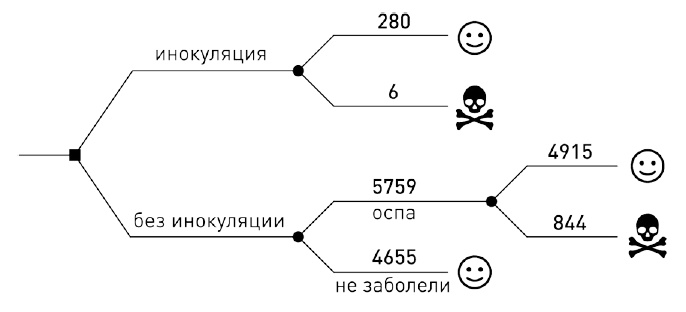
Мы исходим из того, что смертность от оспы, вызванной инокуляцией, и от оспы, полученной естественным путем, остается примерно неизменной от одной вспышки к другой. Поэтому смертность во время первой вспышки соответствует нашим шансам остаться в живых или погибнуть во время следующей.
Конечно, во время первой вспышки оспы этих данных еще не было, и опереться, делая сложный выбор, было не на что. Но благодаря тому, что Мэзер и Бойлстон тщательно собирали сведения о погибших и выживших, уже во время следующей волны инфекции можно было принять правильное решение.
Смертность тех, кто сделал инокуляцию, составила 0,021, выживаемость – 0,979. В сумме шансы этих взаимоисключающих сценариев должны быть равны единице.
Среди тех, кто не делал инокуляцию и заболел оспой естественным путем, смертность была 0,147, а выживаемость 0,853. Доля оставшихся в живых среди тех, кто отказался от инокуляции, складывается из тех, кто не заболел оспой, и тех, кто заболел и выжил. Поэтому вероятность выжить при отказе будет равна 0,919
[88].
Шансы выжить при разных решениях тоже нагляднее представить в виде дерева.
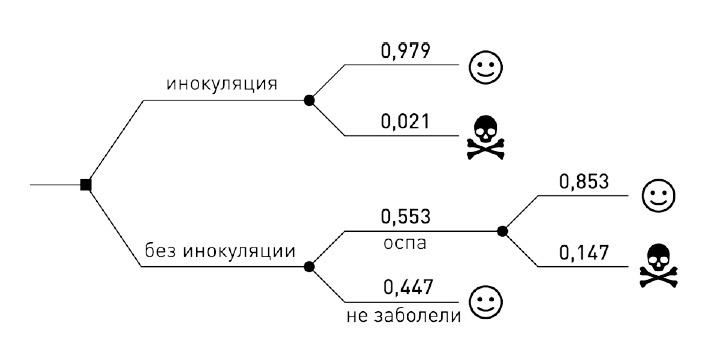
В случае инокуляции шансы выжить несколько выше и равны 0,979. Поэтому процедура была верным выбором, но разница в шансах остаться в живых была не так велика, как может показаться, если сравнивать смертность прошедших инокуляцию и тех, кто заболел оспой естественным путем. Это вызвано тем, что среди прошедших инокуляцию заболевают все, а среди непрошедших доля заболевших лишь 0,553.
Однако мы должны учесть несколько моментов. Во-первых, смертность от оспы в Бостоне была относительно невысока. Это могло быть связано как с высоким уровнем жизни, так и с относительно неагрессивным вариантом вируса-возбудителя. Чем выше смертность от оспы, тем более правильным решением становится инокуляция. Во-вторых, значение 0,553 для заболеваемости в случае отказа от инокуляции занижено, поскольку не учитывает, что эта эпидемия оспы была в Бостоне не первой и многие не заболели, потому что болели раньше и имели иммунитет. Поскольку решение об инокуляции нужно принимать только тем, у кого иммунитета нет, то бостонцев с иммунитетом надлежит исключить при подсчете доли не заболевших. У нас нет данных о том, сколько из 4655 не заболевших имели иммунитет. Но если мы предположим, что хотя бы половина, то шансы выжить, не имея иммунитета и не сделав инокуляцию, были еще меньше и составляли уже 0,896
[89].
Получается, что инокуляция в любом случае была более безопасным выбором
[90].
Ничего страшного, если вы не следили за расчетами. Гораздо важнее понять стоящую за ними идею, оказавшую колоссальное влияние на то, как проводятся медицинские исследования.
Идея заключается в том, что мы можем делать выводы обо всей популяции, то есть о группе объединенных общим признаком людей на основе наблюдения за относительно небольшой ее частью. Например, на основании наблюдений за прошедшими инокуляцию в Бостоне в 1721 году сделать прогноз относительно судьбы тех, кто пройдет инокуляцию во время следующих вспышек оспы как в Бостоне, так и в других городах. Мы считаем всех прошедших инокуляцию одной большой популяцией, у которой достаточно общего, чтобы распространять результаты наблюдения за одной ее частью на остальные. Тех, кто не имел иммунитета и отказался от инокуляции, мы рассматриваем как другую популяцию. Сравнивая смертность в этих двух популяциях, мы можем решить, к какой из них безопаснее принадлежать.
Популяционный подход позволяет сделать прогноз относительно группы людей, но не предсказывает судьбу отдельного человека. Мы знаем, что на тысячу прошедших инокуляцию выживало больше, чем на тысячу отказавшихся. Но ни у Бенджамина Франклина тогда, ни у нас сейчас нет и не может быть способа сказать, что случилось бы именно с его четырехлетним сыном. Как бы ни хотелось нам уметь точно предсказывать судьбу отдельного человека, невероятная сложность биологических систем, к которым относятся и наши тела, не позволяет строить модели, гарантированно предсказывающие будущее. Нам остается оперировать шансами, или вероятностями. Мы еще поговорим об этом в следующих главах.
Бурная дискуссия вокруг инокуляции постепенно приучила врачей к тому, что свою позицию можно и нужно доказывать с помощью чисел. Используя математические аргументы, инокуляцию защищали такие известные врачи, как Филип Пинель, Уильям Блэк, Томас Персиваль и уже знакомый нам по проверке вытягивателей Джон Хайгарт. Хотя большинство продолжало считать числовой метод абсолютно неуместным в медицине, некоторые стали понемногу применять простую арифметику. С ее помощью были оценены эффективность кровопускания при лихорадке, методы лечения психических болезней, связь между болезнями и погодой, а также проведен сравнительный анализ выживаемости при разных способах хирургического удаления почечных камней и при разных наборах показаний для ампутации конечности. Предсказуемо, эти методы нашли больше поддержки в армии и на флоте, чем в гражданской медицине.




