Технические детали такого конструирования нас касаться не должны, поскольку для настоящих целей достаточно простой базовой идеи. Мы начнем с допущения, что у агентов есть предпочтения по отношению не только к вариантам выбора, но к лотереям (lotteries) вариантов, включая выродившуюся лотерею (degenerate lottery), состоящую в безусловном получении базового выигрыша. Для любого конкретного набора вариантов или призов лотерея определяет вероятность получения каждого из них с суммарной вероятностью, равной 1. Предполагается, что агенты в таких лотереях имеют полные и транзитивные предпочтения. Кроме того, считается, что для предпочтений действует аксиома независимости: на предпочтения, оказываемые лотереям p и q, не влияет их комбинирование одним и тем же образом с третьей лотереей r. Эффект определенности, о котором говорилось в главе VII и который будет еще обсуждаться в главе XII, нарушает эту аксиому.
Наконец, предполагается, что предпочтения демонстрируют форму непрерывности, определяемую следующим образом. Предположим, базовые варианты включают лучший элемент А и худший элемент В. Мы произвольно присваиваем им значения полезности 1 и 0. Непрерывность означает, что для любого промежуточного варианта С есть вероятность р (С), которая делает агента безразличным к тому, получить С наверняка или поучаствовать в лотерее, которая даст ему А с вероятностью р (С) и В с вероятностью 1 – р (С)
[166]. Затем мы принимаем кардинальную полезность u (С) равной р (С). Это число является, конечно, произвольным, потому что такими же являются конечные полезности. Предположим, мы присвоим значения М и N соответственно элементам А и В (M > N). Определяем полезность С как ожидаемую полезность лотереи pM + (1 – p) N = Mp – N – N p = (M – N) p + N.
Полученный класс функций полезности гораздо меньше, чем класс функций порядковой полезности
[167]. Легко видеть, что если вариант Х имеет бо́льшую ожидаемую полезность, чем Y, в соответствии с одной функцией, то это же он будет иметь и в соответствии с другой. Так, мы можем с уверенностью утверждать, что рациональный агент максимизирует ожидаемую полезность.
Функции количественной полезности имеют важное свойство линейности по вероятности. Давайте введем обозначение XpY, означающее лотерею, в которой предлагается вероятность р получения Х и (1 – р) получения Y. При использовании шкалы с конечной точкой 1–0 полезность u (X) равна вероятности q, при которой агент у безразлично, выбрать Х или лотерею A q B. Точно так же полезность u (Y) равна вероятности r, при которой агенту безразлично, выбрать Y или лотерею ArB. XpY, таким образом, предлагает полезность, эквивалентную шансу р на получение А с вероятностью q и шансу (1 – р) на получение А с вероятностью r. Таким образом, полезность XpY составляет pq + r (1 – p), то есть p раз полезность Х плюс (1 – р) раз полезность Y. Например, полезность вероятностной комбинации 3 шансов из 5 получить Х и 2 из 5 получить Y равна 3⁄5 q + 2⁄5 r.
Здесь возможны следующие возражения. Предположим, у фермера есть выбор между двумя культурами: традиционной разновидностью, которая с равной вероятностью может дать хороший или средний урожай в зависимости от погоды, и современной, которая с равной вероятностью может дать отличный или плохой урожай. Предположим, количественная полезность 3 и 2 для более старой культуры, 5 и 1 для более новой. Поскольку ожидаемая полезность новой культуры больше, то фермер должен выбрать ее. Но – и в этом суть возражения – разве при этом не упускается из виду то, что фермер может не иметь склонности к риску и неохотно примет любой вариант, допускающий настолько низкий уровень полезности, как 1? Возражение, однако, включает двойной счет, так как нежелание рисковать уже инкорпорировано в построение количественных полезностей. При допущении, что А, В и С получают значения 100, 0 и 60, u (C) вполне может составить 0,75 для человека, не склонного к риску, предполагая, что ему безразлично, получить 60 наверняка или участвовать в лотерее, в которой у него 25 %-й шанс ничего не получить и 75 %-й – получить 100. Подобный аргумент применим к присваиванию значений количественной полезности физическим объемам урожая.
В качестве еще одного примера рассмотрим получения разрешения опеки над ребенком (см. рис. XI.2). Горизонтальная ось может быть понята двояко – как предполагающая физическое разделение опеки (процент времени, проведенного с ребенком) либо вероятностное разделение (шансы получить по суду полную опеку). Количественная полезность равного разделения времени – AE, что больше, чем полезность AC 50 %-й вероятности полной опеки. (Здесь мы апеллируем к тому факту, что количественная полезность линейна по вероятности.) Причина в том, что большинство людей в подобной ситуации демонстрируют нежелание рисковать. Они соглашаются на совместную опеку, потому что 50 %-й риск не иметь возможности видеть ребенка слишком не приемлем. Только если родитель полагает, что его или ее шансы получить полную опеку выше, чем q процентов, судебное разбирательство становится предпочтительнее совместной опеки. Значительное число разбирательств об опеке в судах свидетельствует не о склонности родителей к риску, а о принятии ими желаемого за действительное, выражающемся в переоценке своих шансов на получение полной опеки над ребенком.
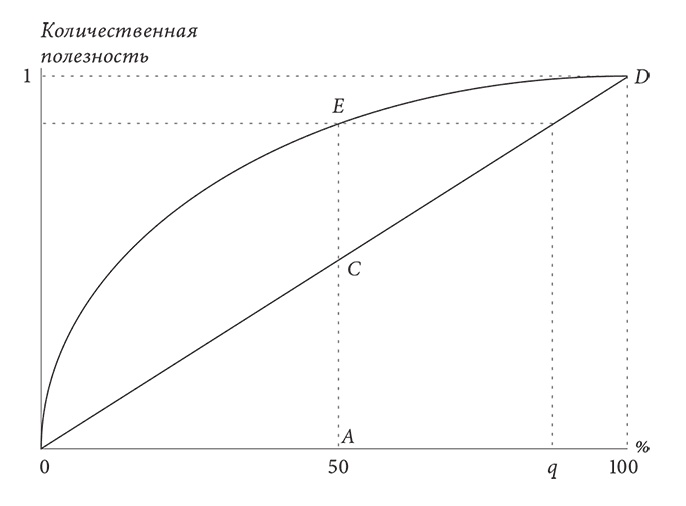
РИС. XI.2
Неприятие риска и убывающая предельная полезность
Несмотря на верность общего хода рассуждений, предшествующее изложение может направить по неверному пути. Некоторые работы на эти темы склонны стирать различие между неприятием риска и уменьшающейся предельной полезностью. Для развития этой идеи мне потребуется ввести концепцию, которая, как подсказывает интуиция, имеет смысл, хотя ее (до сих пор) было нелегко измерить. Это идея внутренней полезности (intrinsic utility) некоего блага, отражающая интенсивность предпочтений агента. Интроспекция со всей очевидностью показывает, что некоторые блага или навыки дают огромное наслаждение, другие – простое удовлетворение, еще одни вызывают легкое раздражение, а какие-то просто ужасны. Очевидно, что представлять различия между ними в категориях количественных предпочтений («Я предпочитаю рай аду точно так же, как я предпочитаю четыре яблока трем») – значит пользоваться крайне обедненным представлением о благополучии или пользе. Тот факт, что у нас нет надежного способа присваивания числовых значений внутренним уровням удовлетворенности или неудовлетворенности, не свидетельствует о безнадежности самой идеи. В равной мере наша неспособность квантифицировать и сравнивать уровни удовлетворенности разных индивидов не доказывает, что идея сравнения межличностного благополучия лишена смысла.



