Тот периметр, на котором вторая космическая сравнялась со скоростью света, становится границей черной дыры, точкой невозвращения, “горизонтом событий”. В конце 1960-х Хокинг и Пенроуз предложили считать черную дыру областью вселенной или “рядом событий”, откуда ничто не может вырваться наружу. Это определение прижилось. Черная дыра, границей которой служит горизонт событий, обнаруживается, лишь когда в пространстве-времени прослеживаются пути космических лучей, которые останавливаются на краю этой сферической границы, не проникая вовнутрь, но и не в силах уйти от нее. Гравитация на таком расстоянии от центра черной дыры достаточно сильна, чтобы не отпустить эти лучи, но недостаточно сильна, чтобы притянуть их ближе. Как же выглядит эта сфера? Словно огромный, мерцающий в космосе шар? Нет. Если фотоны не могут оторваться от орбиты, они не достигают наших глаз. Чтобы мы увидели объект, нужно, чтобы от него до нас долетели фотоны.
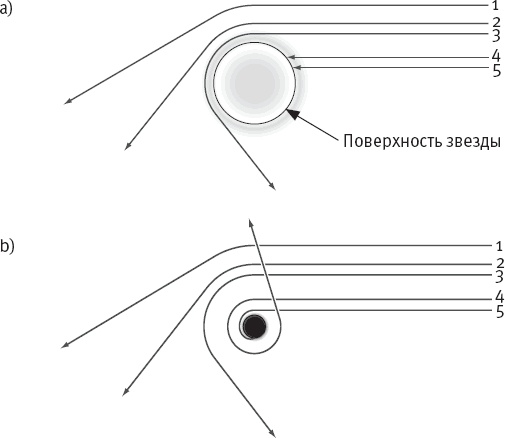
Рис. 5.5. На схеме (а) частицы движутся из космоса к звезде. Пути частиц 1, 2 и 3 искривляются с приближением к звезде: чем ближе к звезде, тем сильнее искривление. Частицы 4 и 5 падают на поверхность звезды. В схеме (b) частицы 1, 2 и 3 отклоняются в точности как прежде, поскольку пространство-время за пределами звезды ничем не отличается от пространства-времени за пределами черной дыры той же массы. (Вспомните пример со сжатием Земли.) Частица 4 вращается вокруг черной дыры и исчезает. Она может совершить множество оборотов. Частица 5 падает в черную дыру.
Классическая теория учит, что черная дыра открывает лишь три свои тайны: свою массу, свой электрический заряд (если он есть) и угловой момент, то есть скорость вращения (если она вращается). Джон Уилер, рисовавший мелом на доске картинки в помощь своим студентам, изображал, как в черную дыру, смахивающую на туннель, проваливаются телевизор, цветок, стул, “известные частицы”, гравитационные и электромагнитные волны, угловой момент, масса, “еще не открытые частицы”, а с другого конца туннеля выходят лишь масса, заряд и угловое движение. Одной из задач Хокинга в начале 1970-х
[95] стала разработка доказательства забавного утверждения Уилера: “У черных дыр нет волос”.
Размеры черной дыры определяются ее массой. Чтобы вычислить радиус черной дыры (расстояние от ее центра, на котором формируется горизонт событий), возьмите ее солярную массу (она примерно такая же, как была у звезды, превратившейся в черную дыру, если только часть массы не была потеряна при коллапсе) и умножьте это число на три – получите расстояние в километрах. Черная дыра с солярной массой, равной десяти, то есть вдесятеро превышающей массу нашего Солнца, формирует горизонт событий с радиусом в тридцать километров. Понятно, что с изменением массы меняется и радиус, меняются размеры черной дыры. Об этой возможности мы поговорим позже.
Задернув занавес на горизонте событий, звезда погружается в полную изоляцию, поскольку излучаемый ею свет, ее образ, который можно было бы наблюдать из другой точки вселенной, не выпускается за эту границу. Пенроуз хотел понять, продолжится ли коллапс звезды и что будет происходить с ней дальше. Он убедился, что в результате описанного выше коллапса вся материя звезды оказывается внутри ее поверхности, в плену нарастающей силы тяжести, и даже если съеживание не происходит вполне гладко, с сохранением идеальной сферической поверхности, коллапс звезды продолжается. В конце концов поверхность достигает нулевого размера, а материя все так же остается внутри. Огромная звезда с десятикратной солярной массой оказывается пленницей не только горизонта событий радиусом в 30 километров, но более того – нулевого радиуса, нулевого объема. Математики и физики называют такой объект сингулярной точкой. В сингулярной точке плотность материи бесконечна, бесконечно искривление пространства-времени, и лучи света не просто наматываются вокруг – они наматываются с бесконечной плотностью.
Общая теория относительности предвидела существование сингулярных точек, но в начале 1960-х мало кто принимал эту идею всерьез. Физики предполагали, что звезда с достаточно большой массой, подвергшись гравитационному коллапсу, возможно, превращается в сингулярную точку. Пенроуз доказал: если вселенная подчиняется общему закону относительности, то не “возможно”, а непременно.
Глава 6
В прошлом у нас – сингулярная точка
Хокинг вдохновился идеей Пенроуза: звезда с достаточно большой массой во время гравитационного коллапса превращается в сингулярную точку. Вместе с Пенроузом и Робертом Джерочем он начал применять понятие сингулярной точки к другим физическим и математическим задачам
[96]. Он был уверен, что эта теория сможет многое объяснить и в происхождении вселенной. То была радостная работа, “со счастливой уверенностью, что все это поприще принадлежит только нам”
[97]. Хокинг понял: если повернуть время вспять, чтобы коллапс обратился в расширение, гипотеза Пенроуза по-прежнему будет верна. Раз, согласно общей теории относительности, на определенном этапе коллапс непременно превращает звезду в черную дыру, то расширяющаяся вселенная должна была начаться с сингулярной точки. Это будет верно в том случае, если вселенная соответствует так называемой “модели Фридмана”. Что представляет собой модель Фридмана?
Выбор Вселенных
Пока Хаббл не доказал, что вселенная расширяется, вера в статическую вселенную (вселенную с неизменными размерами) была настолько прочна, что Эйнштейн, создав к 1915 году общую теорию относительности, предполагавшую в числе прочего нестатичность вселенной, предпочел внести изменения в свою теорию, до такой степени он был убежден в неизменности размеров вселенной. Великий физик дополнил свое уравнение “космологической константой”, уравновешивающей гравитацию. Без космологической константы общая теория относительности утверждала то самое, что мы теперь принимаем за истину: размеры вселенной меняются.
Российский физик Александр Фридман решил принять теорию Эйнштейна в ее первозданном виде, без космологической константы, и на основании этой теории предсказал то, что подтвердит в 1929 году Хаббл: вселенная расширяется.
Фридман исходил из двух предпосылок: 1) вселенная кажется одинаковой, в какую сторону ни глянь, и исключение составляют лишь близкие к нам объекты – очертания галактики Млечного Пути, наша Солнечная система; 2) вселенная выглядит одинаково с любой точки наблюдения во вселенной. Иными словами, космическому путешественнику вселенная все равно будет казаться одинаковой, в каком направлении ни погляди.
Первую предпосылку Фридмана принять нетрудно, а вот со второй нелегко смириться. Мы не располагаем доказательствами ни за ни против. Как говорит Хокинг, “мы соглашаемся с этим утверждением лишь из скромности: странно было бы, если б вселенная выглядела одинаковой во всех направлениях только с Земли, но не из других точек наблюдения”. Странно, однако ведь не вовсе невозможно. Скромность – ничуть не более убедительный аргумент, чем гордыня. И все же физики в большинстве своем согласны с Фридманом.



