
Онлайн книга «Мастерство учителя»
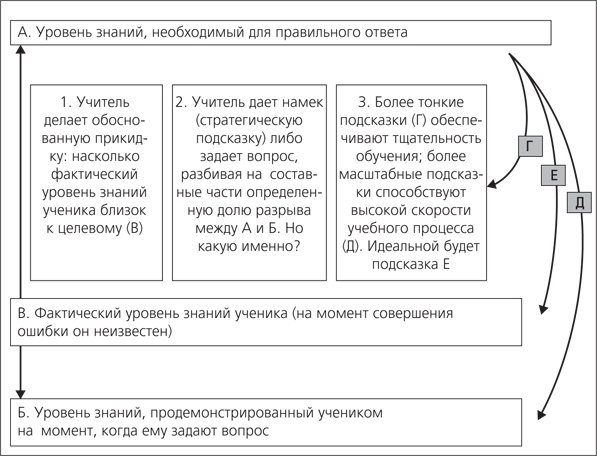
Рис. 3.3. Как работает методика «Разбить информацию на части»
Как видно на этом рисунке, методика «Разбить информацию на части» действительно довольно сложна в применении. Один из лучших способов добиться успеха в этом деле – подготовиться заранее, сделав эту подготовку неотъемлемой частью процесса планирования урока. Для этого следует предварительно выявить потенциально сложные моменты и продумать как наиболее вероятные неправильные ответы, так и возможные подсказки. Еще одно решение – использовать стабильные шаблоны последующих процедур. Такие шаблоны и модели, как правило, дают отличный результат и становятся надежной отправной точкой для решения, как и что надо подсказывать ученикам в том или ином конкретном случае. Способов разбить сложную информацию и задачи на отдельные части существует неограниченное количество, но я опишу шесть проверенных отправных пунктов.
• Привести пример. Если вы попросили ученика дать определение простого числа, а в ответ видите только пустой взгляд, можно сказать: «Таким числом является семь» или «К таким числам относится семь… и одиннадцать». А если вы решили раздробить эту информацию еще больше, можно дать такую подсказку: «Семь – одно из таких чисел, а восемь – нет». Можно пойти и еще на шаг дальше, добавив: «В восьмерке есть сомножители – два и четыре». Понятно, что рано или поздно наступает момент, когда подсказок и намеков в запасе не остается, и тогда вам больше подойдет другая методика, например «Отказ не принимается» ( методика 1 ). Тогда вы говорите, например: «Ребята, кто может сказать Дэвиду, что такое простое число?» А если вопрос, поставивший ученика в тупик, основан на классификации, можно привести дополнительные примеры. Например, пятиклассник из класса Джейми Брилланте никак не мог определить на уроке английского, к какой части речи относится слово owner (владелец). Подобрать пример тут довольно трудно, и учительница вместо этого дала подсказку: «Логически рассуждая, owner, скорее всего, относится к той же части речи, что и другие слова, которые заканчиваются на -er. Dancer, swimmer, singer (танцор, пловец, певец). А это у нас?..» «Это люди», – закончил ученик. «А люди?..» – вопросительно продолжила Джейми. «Люди – это существительное!» – не дал ей закончить фразу мальчик.
• Предложить контекст. Еще один ученик из класса Джейми Брилланте не смог сразу ответить на вопрос, к какой части речи относится слово ancient (древний). Джейми напомнила, что дети уже учили это слово на уроке другого учителя. Подсказка не помогла. «Я надеюсь, что меня пока такой никто не считает, – продолжила учительница. – Ну, может, году в 2080-м вы сможете назвать меня такой, но не раньше». «А-а, древний – это очень-очень старый», – вспомнил ребенок. Тут важно отметить, что Брилланте использует этот подход только в том случае, когда уверена, что класс должен знать данное слово, просто этот ученик его пока не вспомнил.
Данная стратегия, конечно, была бы менее эффективной, если бы учительница не знала, известно ли вообще это слово ребенку и классу. Но когда это точно известно, он очень полезен. Если вернуться к примеру с определением простого числа, учитель, скажем, мог бы отметить, что натуральные числа бывают либо простыми, либо составными. Или вернуться к предыдущему обсуждению: «Мы с вами уже обсуждали простые и составные числа и на какое-то время останавливались на числе восемь». Или: «Как вы помните из нашего обсуждения на прошлой неделе, по сомножителям очень легко определить, простым или сложным является число».
• Напомнить правило. В шестом классе на уроке Кристи Хьюелскамп, которая преподает в Вильямсбургской коллегиальной школе, ученик ошибся, сказав, что слово indiscriminate (неразборчивый) в предложении «Джеймс был неразборчивым читателем: он мог взять в библиотеке любую книгу и прочесть ее от корки до корки» – глагол. Учительница ответила на это правилом: «Глагол обозначает действие или состояние. Разве слово indiscriminate описывает действие?» Мальчик тут же понял, что ошибся, и ответил, что это прилагательное.
• Предложить недостающий (или первый) этап. Когда один из учеников пятого класса не смог объяснить на уроке математики, что не так с написанием числа 15/6, Келли Рагин подсказала: «Что мы всегда делаем, когда числитель больше знаменателя?» Ученик отреагировал мгновенно: «А-а, нам нужно получить смешанное число! Так что мне нужно пятнадцать на поделить шесть».
• Сделать обратный ход. Иногда бывает достаточно просто повторить за учеником неверный ответ. Многие люди сразу признают свою ошибку, если ее воспроизвести так, будто она записана на пленку. Когда ученица из класса Рагин предложила перевести неправильную дробь в смешанное число путем умножения числителя на знаменатель, Келли просто повторила за ней: «Итак, ты говоришь, что мне надо умножить шесть на пятнадцать…» То, какой акцент учительница сделала при этом на слове умножить, наглядно показало девочке, насколько велик разрыв межу ее ответом и правильным вариантом. (Акцент на слове умножить сделал подсказку намного прозрачнее.) В любом случае, большинство из нас быстро понимают, в чем именно ошиблись, услышав, как их неправильный ответ повторяет другой человек.
• Исключить ошибочный выбор. Столкнувшись с тем, что ученик никак не может определить, что слово owner относится к существительным, Брилланте могла исключить некоторые ошибочные варианты выбора, например сказав: «Что ж, давайте обсудим некоторые варианты. Будь это глагол, это слово обозначало бы действие. Разве это так? А как насчет прилагательного? Разве это слово указывает мне на какие-то признаки существительного?»
«Коэффициент»
Одна из важнейших задач учителя – заставить ученика выполнить как можно больше познавательной работы: письменной, предполагающей рассуждения, анализ, обсуждение. Доля когнитивной работы, выполняемой учениками класса, называется коэффициентом участия. (Насколько мне известно, этот термин придумал Дэвид Левин, один из основателей известной во всей стране и достигшей невероятных успехов системы школ KIPP и, по мнению многих, один из самых передовых и эффективных учителей Америки.) Поняв и приняв данную концепцию, вы начнете значительно реже давать окончательное решение задачи без участия детей, например когда складываете числа («Шесть плюс восемь будет… сколько, Сара?»), определяете следующий этап («Что я должен сделать с этой единицей, Джеймс?»), закрепляете в памяти класса ключевые термины («Как называется действие, когда я уменьшаю количество знаков после запятой, Джеймар?») или проверяете выполненное задание. А если один ученик ответит неправильно, вы попросите класс объяснить и исправить ошибку («Валери говорит, что шесть разделить на два будет пять. Это правильно, Рэй?»). Иными словами, ваша цель – дать детям шанс как можно больше упражняться и практиковаться, применить знания в максимальном объеме и проделать при решении задач-образцов всю работу, на которую они способны, вместо того чтобы наблюдать, как это делаете вы, их учитель.
