
Как видно из таблицы, это хорошая игра, потому что при продолжительной игре вы будете выигрывать в среднем $0,33 за каждый раунд. Но что будет, если только 7 останется выигрышным числом? Это повлияет на ожидаемое значение следующим образом.
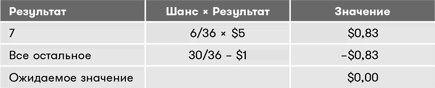
Ноль в графе ожидаемого значения говорит о том, что эта игра похожа на подбрасывание монеты на протяжении долгого времени. Шансы на победу и на поражение абсолютно равны. Давайте теперь вновь изменим правила так, чтобы победной комбинацией было только 11.
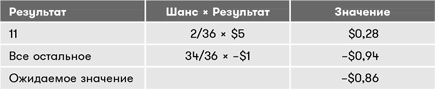
Как вы могли догадаться, в этой игре вы будете обречены на поражение. Вы будете терять в среднем 86 центов за каждый раунд. Конечно, вы можете увеличить свои шансы остаться в плюсе, повысив награду за выпадение 11.
Внимательно взвешивайте значения
Ожидаемое значение – это прекрасный инструмент для настройки игрового баланса, о котором мы поговорим подробнее в следующей главе, но если вы будете не слишком внимательны, рассматривая значения полученных результатов, вы можете пойти по неправильному пути.
Возьмем три типа атаки, которые могут быть частью одной фэнтезийной ролевой игры.
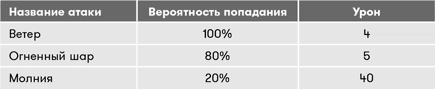
Каким будет ожидаемое значение каждой из этих атак? С ветром все просто – он всегда наносит 4 очка урона, поэтому его ожидаемое значение равно 4. Огненный шар попадает в 80 % случаев и промахивается в 20 %, поэтому его ожидаемое значение (5 × 0,8) + (0 × 0,2) = 4 очка, то есть такое же, как и у ветра. Атака молнией редко достигает цели, но когда все-таки достигает, то разрушает все вокруг. Ее ожидаемое значение – (40 × 0,2) + (0 × 0,8) = 8 очков.
Теперь, исходя из этих значений, можно сделать вывод, что игроки будут всегда использовать атаку молнией, поскольку в среднем она причиняет в два раза больше урона, чем все остальные. И если вам противостоит враг со значением урона 500, такая стратегия себя оправдывает. Но как насчет врагов с уроном 15? Большинство игроков в этом случае не станут использовать молнию, они предпочтут ей что-то слабее, но надежное. Почему так? Ответ таков: несмотря на то что молнией можно нанести 40 очков урона, только 15 из них будут использованы в данной ситуации. Настоящее ожидаемое значение молнии в бою с врагом с 15 очками здоровья – (0,20 × 15) + 0,8 × 0) = 3, что ниже урона, наносимого ветром и огненным шаром.
Вам необходимо иметь четкое представление о реальных значениях для действий в вашей игре. Если что-то дает преимущество, которым игрок не может воспользоваться, или оно подразумевает скрытое наказание, это обязательно нужно учитывать в расчетах.
Человеческий фактор
Также необходимо иметь в виду, что ожидаемые расчеты значений не могут предсказать поведение человека. Вы можете предположить, что игроки будут выбирать преимущественно опцию с самым высоким ожидаемым значением, но так происходит далеко не всегда. В некоторых случаях причина в незнании – игроки просто не знают, что такое ожидаемое значение. Например, не открыв игрокам информацию об относительных шансах ветра, огненного шара и молнии, а предоставив им возможность самостоятельно добывать эту информацию методом проб и ошибок, вы можете заметить, что применившие несколько раз молнию и ни разу не попавшие в цель игроки придут к выводу, что «молния всегда бьет мимо» и поэтому ее ожидаемое значение равняется нулю. Выводы игроков относительно частоты событий как правило бывают ошибочными. Вы должны знать, как игроки воспринимают вероятности в вашей игре, потому что именно они определяют игровой опыт.
Но иногда, даже обладая полной информацией, игроки все равно игнорируют опции с самым высоким ожидаемым значением. Два психолога, Канеман и Тверски, провели интересный эксперимент, в котором спрашивали респондентов о том, в какую игру они хотели бы сыграть.
Игра А
66 % – шанс выиграть $2400
33 % – шанс выиграть $2500
1 % – шанс выиграть $0
Игра Б
100 % – шанс выиграть $2400
Обе игры отличные. Но одинаково ли они хороши? Если сделать расчеты ожидаемого значения…
Ожидаемое значение игры А:
0,66 × $2400 + 0,33 × $2500 + 0,01 × 0 = $2409
Ожидаемое значение игры Б:
1,00 × 2400 = $2400
Как видите, ожидаемое значение игры А чуть выше, чем у игры Б. Но только 18 % участников опроса выбрали этот вариант, тогда как остальные 82 % отдали свое предпочтение игре Б.
Почему? Причина кроется в том, что в расчетах ожидаемого значения нельзя учесть важный человеческий фактор: сожаление. Люди не только склоняются к вариантам, которые доставляют им больше всего удовольствия, но и пытаются избегать тех, которые подразумевают большую вероятность разочарования. Если вы играли в игру А (при условии, что вы играли в нее только раз) и получили $0, вас это сильно расстроит. Люди часто готовы заплатить за то, чтобы уменьшить вероятность разочарования, – «покупают больше мозгов», как говорят продавцы страховых полисов. Несмотря на то что они готовы платить, чтобы избежать разочарования, они еще и готовы рисковать. Поэтому игрок, проигравший немного денег, нередко берет на себя еще больший риск в попытке отыграть деньги обратно. Тверски описал это таким образом: «Когда дело касается заработка, все люди – консерваторы. Вероятному заработку они предпочтут заработок наверняка. Но мы также обнаружили, что, когда люди выбирают между гарантированной потерей и относительно небольшим шансом проиграть по-крупному, они более склонны к риску». Это человеческое свойство сыграло не последнюю роль в успехе условно бесплатной игры Puzzle & Dragons. По мере продвижения через подземелья игроки решают серии головоломок и собирают сокровища. Иногда, правда, они могут погибнуть в подземелье и получить сообщение от игры «Так жаль, что вы погибли. Посмотрите, сколько сокровищ вы сейчас потеряете. Как насчет заплатить немного реальных денег, чтобы сохранить все эти сокровища?» И многие платят, чтобы избежать гарантированной потери своих сокровищ.
Порой человеческий мозг излишне сильно раздувает вероятность некоторых рисков. В одном исследовании Тверски попросил людей оценить вероятность различных причин смерти и получил следующие результаты.
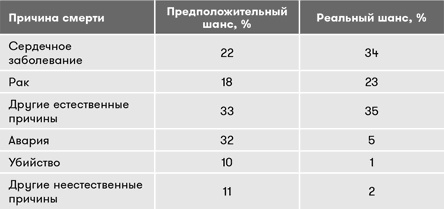
Любопытно, что респонденты в своих оценках недооценили три верхние категории (естественные причины смерти) и значительно переоценили нижние три (неестественные причины смерти). Это искажение реальности можно считать отражением личных страхов респондентов. Но как это можно использовать в геймдизайне? Как дизайнер вы должны иметь контроль не только над реальными вероятностями событий в вашей игре, но и над воспринимаемыми вероятностями, которые не всегда будут соответствовать вашим ожиданиям.







