
Рис. 3.7. Искривленная (двумерная) поверхность
Затем он попросил одного своего талантливого студента обобщить этот подход на искривленные пространства в трех и более измерениях. Этот студент, Бернхард Риман, подготовил обширную диссертацию, которая казалась совершенно бесполезной.
Полученный Риманом результат заключался в том, что свойства искривленного пространства (или пространства-времени) любой размерности описываются определенным математическим объектом, который мы сегодня называем римановской кривизной и обозначаем буквой R. Если представить себе равнинный, холмистый и горный ландшафты, то кривизна R поверхности равна нулю на равнинах, которые являются плоскими («без кривизны»), и отлична от нуля на холмах и в долинах; она достигает максимума на острых горных пиках, то есть там, где поверхность дальше всего от плоской, сильнее всего искривлена. С помощью римановской теории можно описывать форму кривых поверхностей в трех или четырех измерениях.
С огромным трудом, обращаясь за помощью к друзьям, лучше разбирающимся в математике, Эйнштейн освоил теорию Римана и записал уравнение, в котором кривизна R пропорциональна энергии материи. В словесной форме это уравнение можно выразить так: пространство-время сильнее искривляется там, где находится материя. И всё. Это уравнение аналогично уравнениям Максвелла, но применительно к гравитации, а не к электричеству. Оно занимает полстроки, и ничего больше не требуется. Образное представление об искривленном пространстве выражается в этом уравнении.
Внутри этого уравнения заключена целая текучая вселенная. В нем магическая сила теории раскрывается в фантасмагорическом ряду предсказаний, напоминающих бредовые видения сумасшедшего, которые, однако, оказываются истиной. Вплоть до самого начала 1980-х годов почти никто не принимал всерьез большую часть этих фантастических предсказаний. И все же, одно за другим, они подтверждались на опыте. Рассмотрим некоторые из них.
Для начала Эйнштейн вычисляет влияние массы, такой как Солнце, на кривизну окружающего пространства, а затем влияние этой кривизны на движение планет. Он находит, что движение планет соответствует предсказаниям уравнений Кеплера и Ньютона, но не совсем точно: вблизи Солнца влияние кривизны пространства сильнее, чем действие ньютоновской силы. Эйнштейн рассчитывает движение Меркурия, ближайшей к Солнцу планеты, для которой расхождение между его теорией и теорией Ньютона должно быть наибольшим, и находит различие: ближайшая к Солнцу точка орбиты Меркурия смещается каждый год на 0,43 секунды дуги больше, чем предсказывает теория Ньютона. Это очень маленькое различие, но астрономы могли его измерить, и результат сравнения предсказаний с астрономическими наблюдениями был однозначен: Меркурий движется по траектории, предсказанной Эйнштейном, а не Ньютоном. Меркурий, быстроногий посланец богов в крылатых сандалиях, следует за Эйнштейном, а не за Ньютоном.
Таким образом, уравнение Эйнштейна описывает, как искривляется пространство в непосредственной близости от звезды. Из-за этой кривизны свет отклоняется от своей траектории. Эйнштейн предсказывает, что Солнце вызывает искривление проходящего рядом с ним света. В 1919 году производится измерение; полученная величина отклонения света в точности соответствует предсказанию.
Однако искривляется не только пространство, но также и время. Эйнштейн предсказывает, что на Земле время течет быстрее на большей высоте и медленнее – на меньшей. Производится измерение, которое подтверждает этот факт. Сегодня во многих лабораториях есть чрезвычайно точные часы, и этот странный эффект может быть измерен даже для разницы высот всего в несколько сантиметров. Поместите одни часы на пол, а другие на стол, и те, что на полу, покажут, что прошло меньше времени, чем на столе. Почему? Потому что время не универсально и однозначно, оно способно растягиваться и сжиматься под влиянием близко расположенных масс. Земля, как и любая масса, искривляет пространство-время, замедляя течение времени в окружающем ее пространстве. Два близнеца, один из которых живет на уровне моря, а другой в горах, при встрече обнаружат, что один из них старше другого, хотя и совсем ненамного (рис. 3.8).

Рис. 3.8. Двое близнецов провели жизнь в разных местах: один на уровне моря, а другой – в горах. Когда они встретились, тот, кто жил в горах, оказался старше. Так проявляется гравитационное растяжение времени
Этот эффект дает интересное объяснение падению предметов. Если нарисовать на карте мира маршрут, по которому самолет летит из Рима в Нью-Йорк, он не будет выглядеть прямым: самолет описывает дугу, отклоняясь к северу. Почему? Поскольку поверхность Земли искривлена, путь, отклоняющийся к северу, короче, чем проложенный вдоль параллели. Расстояние между меридианами тем меньше, чем севернее вы находитесь; поэтому для сокращения пути лучше отклониться к северу (рис. 3.9).
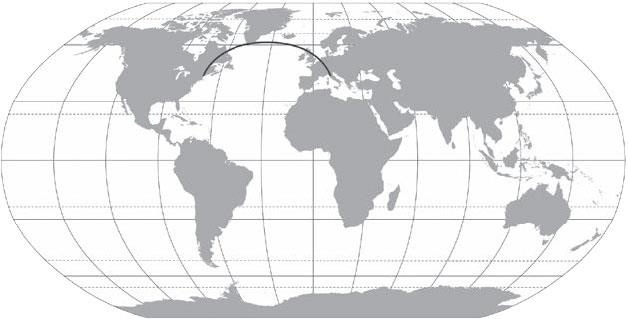
Рис. 3.9. Чем севернее вы находитесь, тем меньше расстояние между двумя меридианами
Так вот, верите вы в это или нет, но брошенный вверх мяч падает вниз по той же самой причине: он «выигрывает время», двигаясь вверх, поскольку время течет там с другой скоростью. В обоих случаях аэроплан и мяч следуют по прямым траекториям в искривленном пространстве (или пространстве-времени) (рис. 3.10)
[53].
Рис. 3.10. Чем выше находится предмет, тем быстрее течет для него время
Однако предсказания теории идут гораздо дальше этих незначительных эффектов. Звезды горят столько времени, на сколько хватает им запасов водорода – их топлива, затем они умирают. Оставшееся вещество больше не поддерживается тепловым давлением и коллапсирует под собственным весом. Когда это происходит с достаточно большой звездой, вес оказывается так велик, что материя сжимается до колоссальной плотности, а пространство искривляется настолько сильно, что в нем образуется настоящая дыра. Черная дыра.






