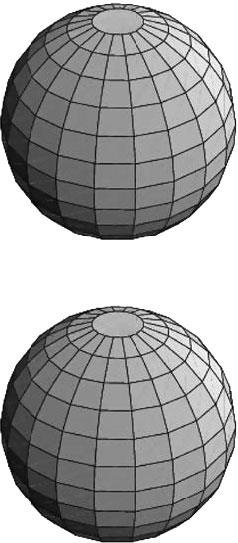
Рис. 3.12. 3-сферу можно представить в виде двух шаров, соединенных друг с другом
Покидая один шар, мы вступаем в другой, точно так же как, покидая один круг карты мира, мы попадаем в другой. Каждый из шаров окружает другой и окружен им. Идея Эйнштейна состоит в том, что пространство может быть 3-сферой – иметь конечный объем (равный сумме объемов двух шаров), но не иметь границ
[62]. В своей работе 1917 года Эйнштейн предложил 3-сферу в качестве решения проблемы границы Вселенной. С этой статьи начинается современная космология, изучение всей видимой Вселенной, рассматриваемой в самом крупном масштабе. Она порождает открытие расширения Вселенной, теорию Большого взрыва, проблему рождения Вселенной и еще много чего другого. Я подробнее расскажу обо всем этом в главе 8.
Есть еще одно замечание, которое я бы хотел сделать относительно эйнштейновской 3-сферы. Может показаться невероятным, но эта идея уже была предложена другим гением из совершенно иной культурной вселенной – великим итальянским поэтом Данте Алигьери. В «Рае», третьей части своей главной поэмы «Божественная комедия», Данте рисует величественный образ средневекового мира, уподобленный миру Аристотеля, со сферической Землей в центре, окруженной небесными сферами (рис. 3.13).
В сопровождении своей сияющей возлюбленной Беатриче, Данте в ходе фантастического мысленного путешествия поднимается по этим сферам до самой внешней сферы. Достигнув ее, он созерцает под собой мир с его вращающимися небесами и Землей далеко внизу в самом центре. Но затем он смотрит вверх – и что же он видит? Он видит светящуюся точку, окруженную огромными сферами ангелов, иными словами – другую колоссальную сферу, которая, по его словам, «окружает и в то же время окружена» сферой нашей Вселенной! Здесь в строках XXVII песни «Рая» он пишет: “Questa altre parte dell’Universo d’un cerchio lui comprende si come questo li altri”
[63], а затем в XXX песни повторяет о последней точке: “parendo inchiuso da quell ch’elli inchiude”
[64]. Точка света и сфера ангелов окружают Вселенную, и в тоже время они окружены Вселенной! Это точное описание 3-сферы!
[65]
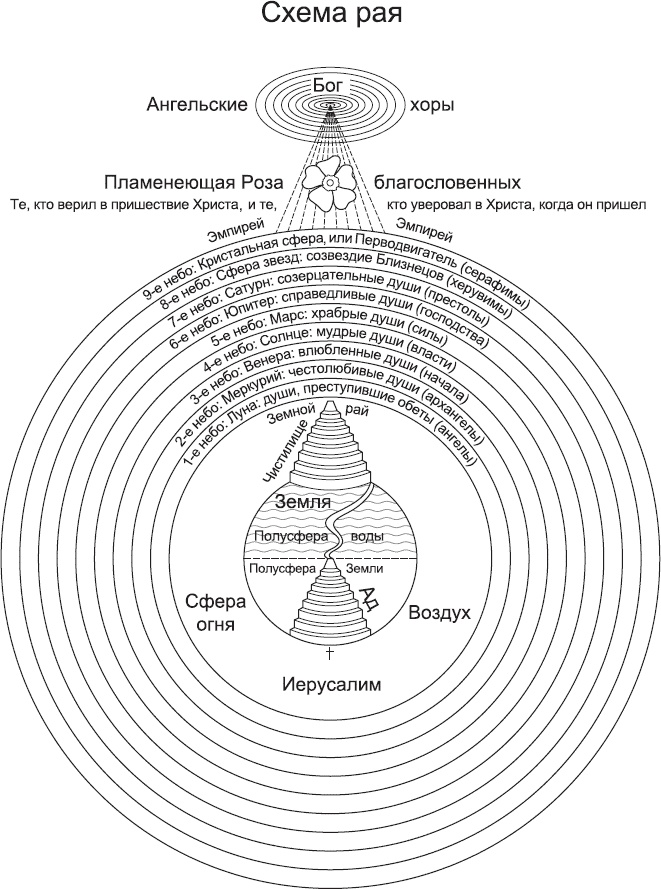
Рис. 3.13. Традиционное представление Вселенной Данте
Американский математик Марк Петерсон в 1979 году первым заметил, что «Рай» описывает Вселенную как 3-сферу. В целом исследователи творчества Данте не очень хорошо знакомы с 3-сферами. Однако любой современный физик или математик легко распознает 3-сферу в дантовском описании Вселенной.
Каким образом Данте могла прийти в голову идея, звучащая столь современно? Я думаю, это в первую очередь отражение глубочайшего интеллекта великого итальянского поэта. Именно его ум делает «Божественную комедию» такой восхитительной. Но также это связано с тем, что Данте писал задолго до того, как Ньютон убедил всех, что бесконечное пространство космоса имеет плоскую евклидову геометрию. Данте был свободен от ограничений, наложенных на нашу интуицию в результате ньютонианского обучения.
Научная культура Данте основывалась главным образом на поучениях его наставника Брунетто Латини, от которого до нас дошел небольшой очаровательный трактат «Li tresor», своего рода энциклопедия средневекового знания, написанная на дивной смеси старофранцузского и итальянского. В «Li tresor» Брунетто подробно объясняет, почему Земля является круглой.
Но он делает это странным для современного читателя способом – в категориях «внутренней», а не «внешней» геометрии. То есть он не пишет, что Земля похожа на апельсин, не говорит, как она выглядит, если смотреть на неё извне, а объясняет ее форму так: «Два рыцаря, которые достаточно далеко проскачут в противоположных направлениях, встретятся на противоположной стороне». И так: «Если бы не мешали моря, человек, начавший идти в одну сторону, вернулся бы в ту же точку Земли, откуда вышел». Иными словами, он использует внутреннюю, а не внешнюю точку зрения – с позиции того, кто идет по Земле, а не того, кто смотрит на нее со стороны. На первый взгляд, это может показаться бессмысленным, усложненным способом объяснения того, что Земля является шаром. Почему Брунетто просто не говорит, что Земля похожа на апельсин? Но с другой стороны, если мы скажем, что муравей ползет по апельсину, то в какой-то момент он окажется в перевернутом положении и должен будет удерживаться крошечными присосками на ногах, чтобы не упасть. Однако путешественник, идущий по Земле, никогда не оказывается в перевернутом положении и не нуждается в присосках на ногах. Так что описание Брунетто на самом деле не такое уж странное.
Теперь задумайтесь над этим. Некто узнал от своего учителя, что форма поверхности нашей планеты такова, что, двигаясь все время по прямой линии, мы возвращаемся в точку, откуда вышли. Вероятно, не так уж трудно сделать следующий очевидный вывод и осознать, что форма всей Вселенной такова, что, двигаясь все время по прямой линии, мы вернемся в ту же точку, из которой отправились: 3-сфера – это пространство, в котором «два крылатых рыцаря, способных лететь в противоположных направлениях, встретятся на противоположной стороне». Выражаясь более формально, описание геометрии Земли, предложенное Брунетто Латини в «Li tresor», дано в терминах внутренней геометрии (рассматриваемой изнутри), а не внешней (рассматриваемой снаружи), и это как раз такое описание, которое подходит для обобщения понятия сферы с двух измерений на три. Лучший способ описания 3-сферы – это не пытаться «увидеть ее снаружи», а описывать то, что происходит, когда вы движетесь внутри нее.
Метод, разработанный Гауссом для описания кривых поверхностей и обобщенный Риманом для описания искривления пространства в трех и более измерениях, в основе своей следует пути Брунетто Латини. Идея, можно сказать, состоит в том, чтобы описывать кривизну пространства не как «видимую со стороны», говоря, как оно искривляется во внешнем пространстве, а в тех понятиях, которые может воспринимать наблюдатель, находящийся внутри этого пространства и способный двигаться, всегда оставаясь в нем самом. Например, обычная сфера, как заметил Брунетто, – это такая поверхность, где все «прямые» линии возвращаются к исходной точке, пройдя одно и то же расстояние (длину экватора). 3-сфера – это трехмерное пространство, обладающее таким же свойством.




