Однако теперь к идеям Фарадея добавляются две новые составляющие.
Первая из них заключается в том, что мы имеем дело с квантовой теорией. В квантовой теории всё дискретно. Это означает, что непрерывная паутина бесконечно тонких параллельных линий теперь становится похожей на реальную паутину: она содержит конечное число отдельных линий. Каждая такая линия, определяющая решение уравнения Уилера – Девитта, описывает одну нить этой паутины.
Второй новый аспект, играющий ключевую роль, состоит в том, что мы говорим о гравитации, а значит, как показал Эйнштейн, речь идет не о полях, погруженных в пространство, но о структуре самого пространства. Фарадеевы линии квантового гравитационного поля – это нити, из которых соткано пространство.
Поначалу исследования концентрировались на этих линиях и на том, как они «сплетаются» в наше трехмерное физическое пространство. На рис. 6.1 представлены первые попытки дать интуитивную картину дискретной структуры пространства, которая из этого получается.

Рис. 6.1. Квантовая версия фарадеевых силовых линий, из которых сплетается трехмерная сеть взаимосвязанных колец (петель)
Вскоре, однако, благодаря интуиции и математическим талантливым молодым ученым, таким как аргентинец Хорхе Пуллин и поляк Журек Левандовски, стало ясно, что ключ к пониманию физики обсуждаемых решений лежит в точках, где эти линии пересекаются. Эти точки называются узлами, а линии между узлами – ребрами. Сеть пересекающихся линий образует так называемый граф – это совокупность узлов, соединенных ребрами, как на рис. 6.3 (с. 179).
Фактически расчеты показывают, что без узлов физическое пространство не имеет объема. Иными словами, объем пространства сидит в узлах графа, а не в его ребрах. Линии связывают вместе отдельные объемы, находящиеся в узлах.
На то, чтобы полностью прояснить получившуюся картину квантового пространства-времени, ушли годы. Потребовалось преобразовать плохо определенный математический аппарат уравнения Уилера – Девитта в более определенную форму, пригодную для вычислений. После этого появилась возможность получать точные результаты. Ключевой технический результат, проясняющий физический смысл наших графов, – это расчет спектров объема и площади.
Спектры объема и площади
Возьмем любую область пространства, например комнату, в которой вы читаете эту книгу, если вы находитесь в комнате. Насколько велика эта комната? Размер комнатного пространства измеряется его объемом. Объем – это геометрическая величина, которая зависит от геометрии пространства, но геометрия пространства – как показал Эйнштейн и рассказывал я в главе 3 – это гравитационное поле. Объем, таким образом, – это свойство гравитационного поля, выражающее, сколько гравитационного поля находится между стенами вашей комнаты. Но гравитационное поле – это физическая величина, которая, как любая другая, подчиняется законам квантовой механики. В частности, как любая физическая величина, объем не может принимать произвольные значения, но только некоторые определенные, как я описывал в главе 4. Список всех возможных значений, если вы помните, называется спектром. А значит, должен существовать спектр объема (рис. 6.2).
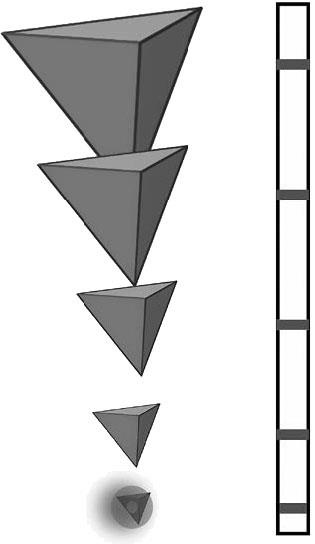
Рис. 6.2. Спектр объема: объем правильного тетраэдра, который физически может существовать, численно ограничен. Наименьший (внизу) – это самый маленький существующий объем
Дирак дал нам формулу, по которой вычисляется спектр любой переменной. Это вычисление требует времени: сначала – чтобы задать его, а затем – выполнить, и это довольно тяжелая работа. Эти расчеты были выполнены в середине 1990-х годов, и, как и ожидалось (Фейнман любил говорить, что мы ничего не должны считать, не зная заранее результат), спектр объема является дискретным, то есть объем может состоять только из дискретных пакетов. Это чем-то похоже на энергию электромагнитного поля, которое тоже складывается из дискретных пакетов – фотонов.
Узлы нашего графа представляют эти дискретные пакеты объема и, как и в случае с фотонами, могут иметь лишь определенные размеры, которые можно вычислить, используя общее квантовое уравнение Дирака
[95]. Каждый узел n в графе имеет свой собственный объем vn, равный одному из значений в спектре объема. Узлы – это элементарные кванты, из которых состоит физическое пространство. Каждый узел графа – это квантовая частица в пространстве. Структура, которая при этом получается, изображена на рис. 6.3.
Ребро – это отдельная квантовая фарадеева линия. Теперь мы понимаем, что они представляют собой: если считать два узла двумя крошечными областями пространства, то они будут отделены друг от друга крошечной поверхностью. Размер этой поверхности – это ее площадь. Это вторая величина после объема, характеризующая квантовую паутину пространства, – площадь, ассоциированная с каждой линией
[96].
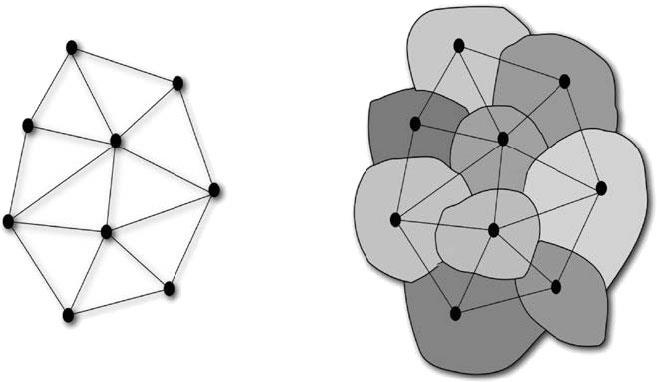
Рис. 6.3. Слева изображен граф, образованный узлами, которые соединены ребрами. Справа – зернистое пространство, которое представлено этим графом. Ребра обозначают смежные частицы, разделенные поверхностями
Эта площадь, как и объем, – физическая переменная, и она имеет спектр, который можно рассчитать, используя уравнение Дирака
[97]. Площадь не является непрерывной величиной, она тоже зерниста. Не существует такой вещи, как произвольно малая площадь.





