То же самое происходит в центре черной дыры: сингулярность классической общей теории относительности исчезает, как только мы принимаем в расчет квантовую гравитацию.
Существует и другого рода ситуация, связанная с электромагнетизмом, в которой квантовая гравитация ставит предел бесконечности. Квантовая теория поля, которую начал создавать Дирак, а завершили в 1950-х годах Фейнман с коллегами, хорошо описывает эти силы, но полна математических нелепостей. При ее использовании для расчета физических процессов мы часто получаем бесконечные бессмысленные результаты. Они называются расходимостями. Расходимости потом исключаются из расчетов с помощью странной технической процедуры, приводящей к конечным итоговым результатам. Этот метод работает на практике и дает верные значения, которые воспроизводятся в экспериментальных измерениях. Но почему теории приходится продираться через бесконечности, чтобы прийти к осмысленным числам?
В последние годы своей жизни Дирак был крайне разочарован бесконечностями в своей теории и, судя по всему, чувствовал, что его цель – истинное понимание того, как устроен мир, – не была достигнута. Дирак любил концептуальную ясность, даже если очевидное для него не всегда было ясно другим. Но бесконечности не способствуют ясности.
Однако бесконечности квантовой теории поля вытекают из лежащего в ее основании допущения о бесконечной делимости пространства. Например, для расчета вероятности различных исходов процесса мы суммируем, как учит нас Фейнман, по всем путям, по которым может разворачиваться этот процесс, а их число бесконечно, поскольку они могут проходить по каждой из бесконечного числа точек пространственного континуума. Именно поэтому мы получаем бесконечные результаты.
Если же принять во внимание квантовую гравитацию, эти бесконечности тоже исчезают. Причина очевидна: пространство не бесконечно делимо, соответственно, не существует бесконечного числа точек и не нужно суммировать по бесконечному числу вариантов. Зернистая, дискретная структура пространства преодолевает трудности квантовой теории поля, исключая бесконечности, которые так ей досаждают.
Это поразительный результат: с одной стороны, учет квантовой механики снимает проблемы, вызываемые бесконечностями в эйнштейновской теории гравитации, то есть избавляет от сингулярностей. С другой стороны, учет гравитации снимает проблемы, порождаемые квантовой теорией поля, то есть избавляет от расходимостей. Вместо того чтобы противоречить друг другу, как казалось первоначально, эти две теории взаимно разрешают проблемы друг друга!
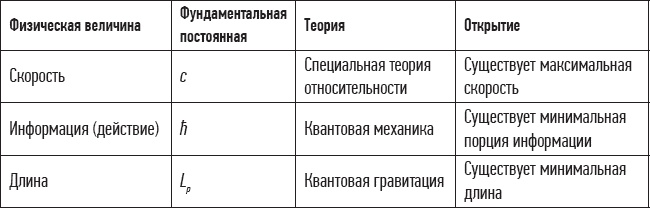
Избавление от бесконечностей – это постоянно повторяющаяся тема в современной физике. Суть специальной теории относительности можно выразить как существование максимальной скорости для физических систем. Суть квантовой механики состоит в открытии существования максимального количества информации для каждой физической системы. Минимальное расстояние – это планковская длина Lp, максимальная скорость – скорость света c, а полная информация определяется постоянной Планка h. Всё это сведено в табл. 11.1.
Существование минимальных и максимальных значений для длины, скорости и действия задает естественную систему единиц. Вместо измерения скорости в километрах в час или метрах в секунду мы можем измерять ее в долях скорости света. Можно принять, что 1 для скорости соответствует скорости c и, например, писать v = 1/2для тела, движущегося со скоростью, равной половине скорости света. Аналогично можно по определению договориться измерять расстояние в единицах планковской длины. Таким образом, мы получаем естественную систему фундаментальных единиц, из которых выводятся все остальные. Единица времени – это время, за которое свет проходит планковскую длину, и т. д. Эти естественные единицы широко применяются в исследованиях по квантовой гравитации.
Таблица 11.1. Фундаментальные ограничения, открытые теоретической физикой
Выявление этих трех фундаментальных постоянных ставит предел тому, что кажется бесконечными возможностями природы. Оказывается, то, что мы называем бесконечным, – это зачастую лишь то, что мы еще не сумели подсчитать или понять. Я думаю, это весьма общая истина. Таким образом, «бесконечное» – это слово, которым мы называем то, чего еще не знаем. Природа, похоже, ясно говорит нам, что ничего подлинно бесконечного не существует.
Есть еще одна бесконечность, дезориентирующая наше мышление, – бесконечность пространственной протяженности космоса. Но, как я писал в главе 3, Эйнштейн обнаружил, что можно представить себе конечный космос без границ. Современные измерения показывают, что размер этого космоса должен быть больше 100 миллиардов световых лет. Это порядок величины той области космоса, к которой у нас есть хотя бы косвенный доступ. Эта величина примерно в 10120 раз больше постоянной Планка и выражается единицей, за которой следует 120 нулей. Между планковским и космологическим масштабами – огромная разница в 120 порядков величины. Колоссальная. Экстраординарная. Но конечная.
В этом диапазоне – начиная с крошечных квантов пространства и далее проходя последовательно кварки, протоны, атомы, химические структуры, горы, звезды, галактики (каждая из которых образована сотней миллиардов звезд), скопления галактик, вплоть до кажущейся бескрайней видимой Вселенной, содержащей более 100 миллиардов галактик, – разворачивается вся сложность нашего мира. Мира, который мы знаем лишь в некоторых его аспектах. Необъятного. Конечного.
Космологический масштаб отражается в значении космологической постоянной Λ, которая входит в фундаментальные уравнения наших теорий. Таким образом, фундаментальная теория содержит очень большое число: отношение космологической постоянной к планковской длине. Именно это огромное число делает возможной колоссальную сложность нашего мира. Но то, что мы видим и понимаем в нашей Вселенной, – это не бесконечность, в которой можно утонуть. Это огромное море, но имеющее конечный размер.
Книга премудрости Иисуса, сына Сирахова (Сирах)
[115], начинается изумительным вопросом:
Песок морей и капли дождя
и дни вечности кто исчислит?
Высоту неба и широту земли,
и бездну и премудрость кто исследует?
Другой великий текст, написанный спустя некоторое время после того, как были сочинены эти строки, вторит им в своих первых словах:



