Логнормальное распределение
Хотя этого не видно на первый взгляд, гауссиану все же можно использовать для описания распределения, представленного на илл. 9. Если отложить доходы по логарифмической шкале, так, чтобы расстояние от $1 до $10 по оси x было таким же, как расстояние от $10 до $100 и так далее, то кривая превратится в аккуратное, точное распределение Гаусса. Мы называем такие распределения логарифмически нормальными, или, сокращенно, логнормальными, потому что они выглядят как нормальное распределение, но в логарифмическом масштабе. Хотя действительно крупные доходы существуют, они не принадлежат к миру Диконии, потому что распределение Гаусса по-прежнему весьма хорошо их моделирует. Мы все еще не покинули пределов Тихонии.
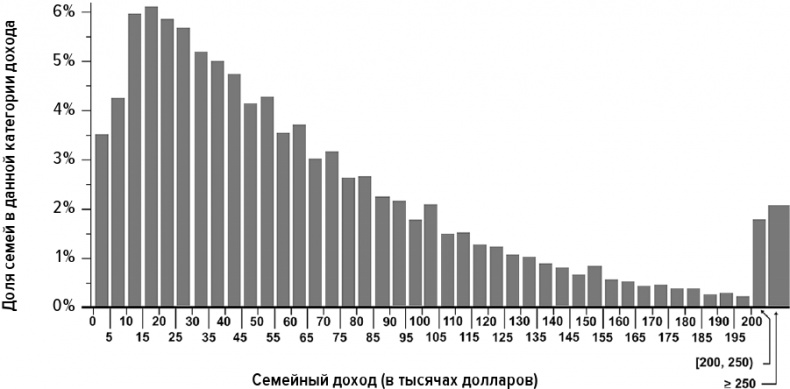
Илл. 9. Распределение семейных доходов в США, 2010 г.
(График Йожефа Бенце, на основе данных интернет-сайта Бюро переписи населения США)
При помощи логарифмической шкалы математики сумели получить новую версию центральной предельной теоремы
[48]. Если некоторая характеристика определяется несколькими слабыми компонентами, причем между этими компонентами нет достаточно сильной взаимозависимости и на одном конце распределения (левом или правом) существует естественная граница, не допускающая возникновения бо́льших или меньших значений, а на другом конце такого предела нет, то распределение этой характеристики по всей генеральной совокупности будет логнормальным.
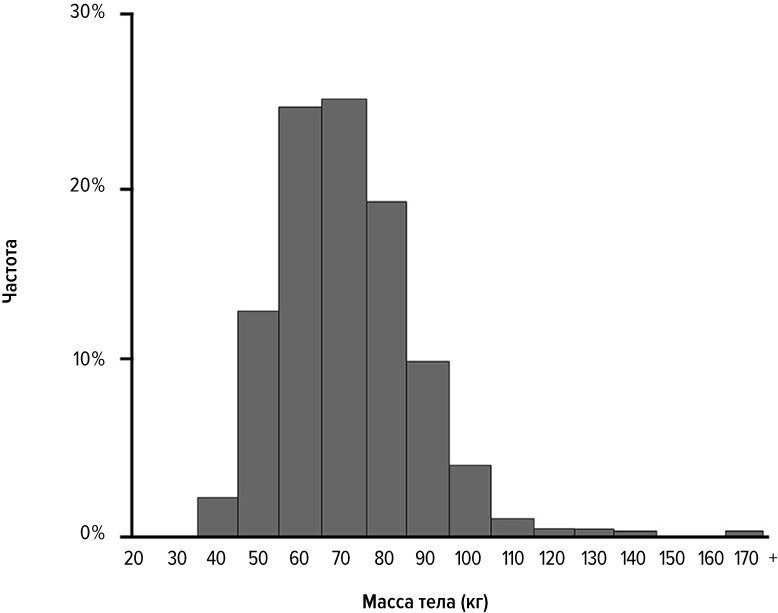
Илл. 10. Распределение массы тела взрослых мужчин в Соединенных Штатах на 2010 г.
(График Йожефа Бенце, на основе данных интернет-сайта Cancer Network)
Масса тела является почти такой характеристикой, но все же не вполне. Разумеется, масса не может быть отрицательной, так что у нее имеется естественный нижний предел, но она ограничена и сверху, хотя верхняя граница находится дальше от среднего значения. На илл. 10 показано распределение массы тела взрослых мужчин в Соединенных Штатах на 2010 год. Этот график представляет собой нечто среднее между нормальным и логнормальным распределениями. Масса тела также принадлежит к миру Тихонии, даже если некоторые люди весят по 270 кг. Не следует считать вес таких людей чудом, так же как нельзя назвать состояние человека, имеющего миллионы долларов, чудесным богатством. Они попросту находятся на окраинах Тихонии. Это утверждение в целом соответствует истине, но, как мы увидим впоследствии, крайне большие доходы следует отнести к явлениям диконским.
Принцип Парето
Итальянский социолог и экономист Вильфредо Парето (1848–1923) также изучал распределение доходов, и именно он первым применил концепцию социальной элиты. Парето, вероятно, не был знаком с логнормальным распределением и поэтому попытался разработать для описания доходов свою собственную модель. Он получил формулу, дававшую относительно хорошее приближение наблюдаемого распределения крупных доходов, но доходам ниже среднего уровня она соответствовала хуже. По-видимому, этот недостаток его не беспокоил. Формула Парето не имеет ничего общего с формулой логнормального распределения, хотя в области больших значений кривая, которую она описывает, получается весьма похожей на кривую этого распределения.
Математики и экономисты все еще спорят о том, что́ лучше описывает реальное распределение высоких доходов — распределение Парето или логнормальное распределение
[49]. Кроме того, они создали несколько других формул, которые хорошо работают в разных контекстах. Впрочем, одно не вызывает сомнений. Хотя формула распределения Парето даже проще, чем формула логнормального распределения, она не обладает всеми теми замечательными математическими свойствами, о которых мы говорили до сих пор: к ней неприменима никакая центральная предельная теорема и она не обеспечивает никакой стабильности. На взгляд математика, распределение Парето выглядит как дело рук шарлатана. Тем не менее заслуг Парето отрицать нельзя, потому что его формула непреднамеренно предсказала науку Диконии. Однако прежде, чем мы сможем существенно углубиться в этом направлении, нам нужно познакомиться с некоторыми диконскими явлениями. Хотя математики и воротили нос от формулы Парето, считая ее недостаточно строгой математически, и не интересовались практическими аспектами его работы, он открыл одно важное правило, касающееся распределения доходов. Правда, как оказалось, его выводы можно было более точно доказать в терминах логнормального распределения, чем распределения Парето.
Парето заметил, что около 80 % совокупного семейного дохода приходится приблизительно на 20 % всех семей. Илл. 9 демонстрирует, что около 20 % семей в Соединенных Штатах имеют доход более $100 000, а если поработать с данными еще немного, можно вычислить, что эти семьи действительно получают около 80 % всего годового дохода.
Парето обнаружил, что такой перекос равновесия действует не только в отношении доходов, но и в отношении размеров богатства и многих других типов ресурсов. Более того, выяснилось, что его наблюдение справедливо в применении к целому ряду, казалось бы, не связанных друг с другом явлений. В большинстве стран около 80 % населения живут приблизительно на 20 % заселенной территории. Около 80 % совокупной массы Галактики распределены среди 20 % ее звезд. Около 80 % нефтяных месторождений находятся на 20 % поверхности Земли. Около 20 % лесных пожаров уничтожают 80 % всех деревьев, сгорающих в пожарах. Этот список можно продолжать дальше и дальше
[50]. Идея о том, что около 80 % результатов можно приписать всего лишь 20 % усилий, стала известна под названием принципа Парето, или «правила 80/20».
Одна из причин, по которым логнормальное распределение (такое, как мы видели в распределении доходов) не принадлежит к миру Диконии, заключается в том, что, хотя оно несимметрично, у него есть стандартное отклонение. В случае логнормального распределения, естественная граница на одном конце которого (например, нулевая нижняя граница в распределении доходов) находится приблизительно в двух стандартных отклонениях от среднего, действует правило 80/20.
Таким образом, логнормальное распределение не только образует теоретическую основу принципа Парето, но и говорит нам, в каких случаях принцип Парето применим. Если некоторое явление определяется несколькими компонентами, ни один из которых не подавляет остальные, и у его распределения существует естественный нижний или верхний предел, расположенный приблизительно в двух стандартных отклонениях от среднего, а с другой стороны естественного предела нет, то для такого явления справедлив принцип Парето. Этот набор требований кажется очень строгим, но ему соответствует на удивление широкий спектр явлений. В число конкретных примеров, которые часто приводят в руководствах по бизнесу и управлению, входят следующие:




