Элеаты впервые открыли различие, а иногда и противоречие между являющимся, φαινομενον
[36], и мыслимым, νοουμενον
[37] [здесь не может быть и речи о кантовском злоупотреблении этими греческими терминами, которое я критикую в приложении], и многообразно воспользовались этим для своих философем и для своих софизмов. По их стопам впоследствии пошли мегарцы, диалектики, софисты, новые академики и скептики. Они обратили внимание на призрачность, т. е. обман чувств, или, скорее, рассудка, превращающего данные чувств в созерцание; этот обман часто заставляет нас видеть такие вещи, которым разум уверенно отказывает в реальности, – например, переломленную палку в воде и т. п. Было понятно, что чувственному созерцанию нельзя доверять безусловно, и отсюда поспешно заключили, будто одно лишь разумное логическое мышление служит порукой истины, хотя Платон (в «Пармениде), мегарцы, Пиррон и новые академики показали на примерах (как позднее в том же роде Секст Эмпирик), что, с другой стороны, умозаключения и понятия тоже вводят в заблуждение и даже влекут за собой паралогизмы и софизмы, которые возникают гораздо легче и разрешаются гораздо труднее, чем призрачность в чувственном созерцании. И тем не менее, рационализм, возникший в противовес эмпиризму, одержал верх, и в соответствии с ним Евклид обработал математику, поневоле обосновывая наглядной очевидностью (φαινομενον) только одни аксиомы, а все остальное – умозаключениями (νοουμενον). Его метод господствовал в течение всех веков, и этому не было бы конца, если бы не было установлено различие между чистым созерцанием а priori и эмпирическим созерцанием. Впрочем, уже комментатор Евклида Прокл, по-видимому, вполне сознавал эту разницу, как показывает у него то место, которое Кеплер перевел на латинский язык в своей книге De harmonia mundi; но Прокл не придал этому вопросу достаточной важности, поставил его слишком изолированно, остался незамеченным и не достиг цели. Только две тысячи лет спустя учение Канта, которому суждено провести столь великие перемены во всем знании, мышлении и деятельности европейских народов, оказало такое же влияние и на математику. Ибо лишь после того, как этот великий ум научил нас, что созерцания пространства и времени совершенно отличны от эмпирических, вполне независимы от всякого воздействия на чувства и обусловливают его, а не обусловливаются им, т. е. априорны и потому совсем недоступны иллюзиям чувств, – лишь после этого мы в состоянии понять, что логические приемы Евклида в математике являются ненужной предосторожностью, костылем для здоровых ног, что они подобны путнику, который, приняв ночью ясный, твердый путь за воду, боится ступить на него и все время ходит около по ухабистой почве и рад время от времени наталкиваться на мнимую воду. Лишь теперь мы можем с уверенностью утверждать, что то необходимое, что представляется нам при созерцании какой-нибудь фигуры, вытекает не из ее чертежа на бумаге, быть может, очень дурно исполненного, и не из абстрактного понятия, мыслимого при этом, а непосредственно из а priori известной нам формы всякого познания. Эта форма везде – закон основания; здесь она как форма созерцания, т. е. пространство, является законом основания бытия; но очевидность и значение его так же велики и непосредственны, как очевидность и значение закона основы познания, т. е. логическая достоверность. Поэтому нам нет нужды и не следует доверять только последней и покидать свойственную математике сферу для того, чтобы искать ей подтверждение в совершенно чуждой для нее области понятий. Оставаясь на свойственной математике почве, мы получаем то великое преимущество, что здесь знание того, что нечто обстоит так, совпадает со знанием того, почему это так, – между тем как евклидовский метод совершенно разделяет оба эти знания и дает лишь первое, а не последнее. Аристотель прекрасно говорит в Analyt. post.I, 27: «Знание сразу и о том, что есть, и о том, почему есть, более точно и первично, чем отдельно знание о том, что есть, и о том, почему есть». Ведь в физике мы только тогда испытываем удовлетворение, когда знание, что нечто обстоит так, соединяется со знанием, почему это так; что ртуть в торричеллиевой трубке подымается на высоту 28 дюймов, – это плохое знание, если не прибавить к нему, что ртуть держится на такой высоте противодействием воздуха. Почему же в математике мы должны довольствоваться тем qualitas occulta
[38] круга, что отрезки каждых двух пересекающихся в нем хорд всегда образуют равные прямоугольники? Что это так, Евклид в самом деле доказывает в 35-й теореме третьей книги; но почему это так, еще неизвестно. Точно так же и Пифагорова теорема знакомит нас с qualitas occulta прямоугольного треугольника; ходульное, даже коварное доказательство Пифагора оставляет нас беспомощными при вопросе почему, между тем как прилагаемая уже известная нам простая фигура при первом же взгляде на нее уясняет дело гораздо лучше этого доказательства и внушает глубокое внутреннее убеждение в необходимости этого свойства и его зависимости от простого угла.
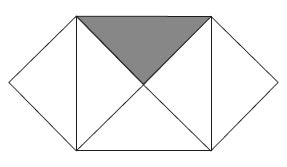
И при неравных катетах должна существовать возможность такой же наглядной убедительности, как и вообще при всех возможных геометрических истинах, – уже потому, что открытие подобной истины вытекало из такой созерцаемой необходимости, а доказательство придумывалось лишь только потом. Поэтому нужно лишь проанализировать ход мысли, совершенный при первом открытии геометрической истины, чтобы наглядно понять ее необходимость. Вообще я желал бы, чтобы математика преподавалась с помощью аналитического метода вместо синтетического, который применял Евклид. Правда, для сложных математических истин это было бы сопряжено с очень большими, хотя и не непреодолимыми трудностями. В Германии в разных местах уже начинают изменять преподавание математики и чаще идут по этому аналитическому пути. Решительнее всех это сделал г. Козак, учитель математики и физики в Нордхаузенской гимназии: к программе экзаменов 6 апреля 1852 г. он присоединил обстоятельную попытку изложения геометрии по указанным мною принципам.
Для улучшения математического метода в особенности необходимо отрешиться от предрассудка, будто доказанная истина имеет какие-то преимущества сравнительно с познанной наглядно, или будто логическая истина, основанная на законе противоречия, лучше метафизической, которая непосредственно очевидна и к которой принадлежит также чистое созерцание пространства.
Самое достоверное и повсюду необъяснимое, это – содержание закона основания. Ибо он в своих различных видах выражает всеобщую форму всех наших представлений и познаний. Всякое объяснение – это сведение к нему, указание в отдельном случае на выражаемую им вообще связь представлений. Он является, следовательно, принципом всех объяснений и потому сам не поддается объяснению и не нуждается в нем, так как всякое объяснение уже предполагает его и лишь через него получает свое значение. При этом ни один из его видов не имеет преимущества перед другими: он равно достоверен и недоказуем как закон основания бытия, или становления, или действия, или познания. Отношение основания к следствию как в одном, так и в других его видах имеет необходимый характер; оно вообще является источником и единственным смыслом понятия необходимости. Не существует другой необходимости, кроме той, что необходимо следствие, если дано основание, и не существует основания, которое не влекло бы за собой необходимости следствия. И подобно тому, как несомненно из данного в посылках основания познания вытекает выражаемое в заключении следствие, так же несомненно основание бытия в пространстве; если я наглядно понял соотношение двух последних, то его несомненность так же велика, как и любая логическая достоверность. А выражением такого соотношения и служит каждая геометрическая теорема, – не менее, чем какая-нибудь из двенадцати аксиом: ведь теорема представляет собой метафизическую истину и таковая столь же непосредственно достоверна, как и самый закон противоречия, являющийся металогической истиной и общей основой всякого логического доказательства. Кто отрицает наглядно представленную необходимость пространственных отношений, выражаемых в какой-либо теореме, тот может с одинаковым правом отрицать и аксиомы, с одинаковым правом отрицать вывод заключения из посылок и даже самый закон противоречия: ибо все это – одинаково недоказуемые, непосредственно очевидные и а priori познаваемые отношения. Поэтому, если наглядно познаваемую необходимость пространственных отношений хотят непременно выводить путем логического доказательства из закона противоречия, то это похоже на то, как если бы непосредственному владельцу земли кто-то другой захотел отдать ее сперва в ленное владение. Именно так поступает Евклид. Только свои аксиомы он поневоле обосновывает непосредственной очевидностью; все же последующие геометрические истины подвергаются логическому доказательству, основанному либо на предпосылке этих аксиом и согласии со сделанными в теореме допущениями или с какой-нибудь прежней теоремой, либо на том, что противоположность теоремы противоречит допущениям, аксиомам, прежним теоремам или даже самой себе. Но аксиомы не имеют большей непосредственной очевидности, чем любая другая геометрическая теорема: они только проще, потому что менее содержательны.



