Что ж, а теперь давайте рассмотрим пример.
Программа геометрической аналогии
Все мы знаем, какой огромный прорыв произошел в том, что касается скорости и мощности компьютеров. Однако не так широко известно, что в других отношениях компьютеры не так уж существенно отошли от своих базовых возможностей. Чаще всего предполагалось, что компьютеры, изначально созданные для выполнения высокоскоростной арифметики, будут заниматься только этим, – вот почему их недальновидно окрестили «вычислительными машинами».
Тем не менее люди вскоре начали писать программы для работы в сферах, не связанных с математикой, таких как лингвистика, графические изображения и различные типы рассуждений. Также вместо следования жестким алгоритмам в некоторые из этих программ была заложена функция поиска среди широкого спектра различных возможных действий – для того чтобы они могли решать часть своих задач методом «проб и ошибок», а не с помощью предварительно запрограммированных шагов. Некоторые из этих ранних «нечисловых» программ стали мастерами в решении головоломок и игр, а иные накопили немало опыта разработки новых устройств и схем
[86].
Однако, несмотря на столь впечатляющие достижения, было ясно, что каждая из этих ранних программ-«экспертов» по решению проблем способна функционировать лишь в рамках конкретной узкой области. Многие наблюдатели пришли к выводу, что причина кроется в неких ограничениях, свойственных самим компьютерам. Они заявили, что компьютер способен решать только «четко определенные задачи» и ему не под силу распознавать двусмысленность или использовать аналогии, что делает человеческое мышление столь универсальным.
Чтобы провести аналогию между двумя вещами, нужно найти, чем они похожи, – но когда и как мы понимаем, что две вещи похожи? Предположим, у них есть некие общие черты, но также есть и отличия. Тогда степень их схожести будет зависеть от того, какие различия мы решим игнорировать. Но ценность каждого отличия зависит от ваших текущих намерений и целей. Например, важность формы, размера, веса или стоимости вещи зависит от того, как мы планируем ее использовать, – то есть аналогии, которые мы проводим, зависят от наших текущих целей. Но до того, как появилась идея разностной машины, мало кто верил, что машины можно наделить целями или стремлениями.
Читатель: Но если ваша теория человеческого мышления опирается на использование аналогий, разве машина на это способна? Мне всегда говорили, что машины могут выполнять только логические операции или решать точно определенные проблемы – а не разбираться с туманными аналогиями.
Чтобы развеять подобные заблуждения, Томас Г. Эванс (1963) написал программу, которая на удивление хорошо показала себя в ситуациях, которые многие люди назвали бы двусмысленными и туманными. В частности, она отвечала на вопросы из широко известного «теста на интеллект», относящиеся к «геометрическим аналогиям». Например, человеку показывают картинку, приведенную ниже, и просят выбрать ответ на вопрос: «К какому из этих пяти рисунков В относится так же, как A относится к Б?» Большинство взрослых людей выбирают цифру 3 – так поступила и программа Эванса, заработавшая на этих тестах примерно такую же оценку, как типичный 16-летний подросток.
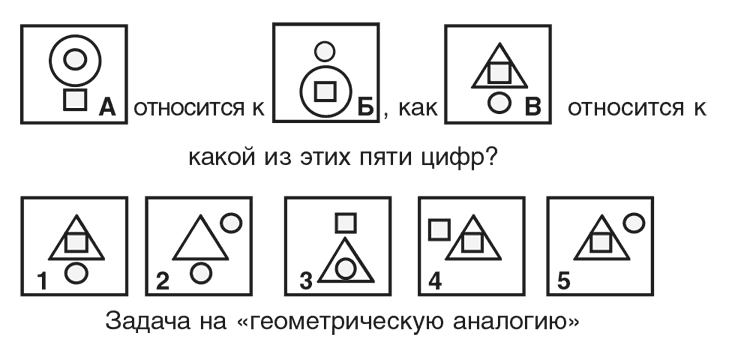
В те дни многим мыслителям было трудно представить, что компьютер способен решать такие задачи, поскольку им казалось, что люди находят ответ на нее с помощью некоего «интуитивного» чувства, которое невозможно воплотить в логических правилах. Тем не менее Эванс нашел способ сделать задачу гораздо менее загадочной. У нас не получится описать здесь его программу во всех деталях, поэтому мы покажем лишь, в чем его методы напоминают то, как действует в таких ситуациях человеческое мышление. Если спросить людей, почему они выбрали цифру 3, они обычно дают такой ответ:
А можно превратить в Б, переместив большой круг вниз,
и
В можно превратить в 3, переместив большой треугольник.
От слушателя ожидается понимание того, что оба предложения описывают что-то общее, несмотря на то, что на рисунке 3 нет большого круга. Однако более красноречивый человек мог бы сказать:
А можно превратить в Б, переместив самую большую фигуру вниз,
и
В можно превратить в 3, переместив самую большую фигуру вниз.
Теперь эти два предложения идентичны, и это говорит о том, что в решении задачи можно было бы использовать трехэтапный процесс, основанный на подобных описаниях. Во-первых, придумайте описания для каждого из верхних рисунков. Например, они могут звучать так:
На рисунке A изображены объекты: крупный сверху, маленький сверху и маленький снизу.
На рисунке Б изображены объекты: крупный снизу, маленький сверху и маленький снизу.
На рисунке В изображены объекты: крупный сверху, маленький сверху и маленький снизу.
Затем нужно придумать объяснение тому, как A можно превратить в Б. Например, просто:
Изменить «крупный сверху» на «крупный снизу».
Наконец, используйте этот алгоритм, чтобы изменить описание рисунка В. Результат будет таков:
На рисунке В изображены объекты: крупный снизу, маленький сверху и маленький снизу.
Если это предсказание того, как изменится рисунок В, соответствует одному из возможных вариантов более точно, чем остальным, именно его мы и выберем в качестве ответа! На самом деле оно соответствует только рисунку 3, который и выбирает большинство людей. (Если оно соответствует двум или более рисункам, программа Эванса начинает весь цикл заново, составляя новые описания тех же изображений.) В итоге она показала на тестах этого типа примерно такой же результат, как обычные пятнадцатилетние подростки.
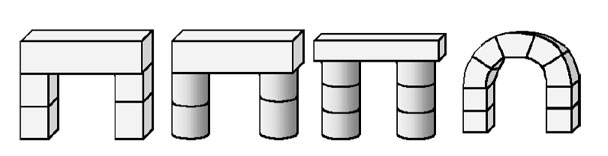
Конечно, когда требуется сделать выбор, нас больше всего занимают различия, имеющие отношение к нашим целям. Если Кэрол хочет просто построить арку, то все варианты на рисунке ниже могут показаться подходящими, но, если она планирует положить на арку сверху еще какие-то фигурки, та, что справа, окажется уже не такой удобной.
Хотя эти конкретные задачки на «геометрическую аналогию» не очень распространены в повседневной жизни, программа Эванса демонстрирует, как важно уметь корректировать свои описания до тех пор, пока не найдешь способа описать разные вещи так, чтобы они казались похожими. Благодаря этому нам часто удается использовать знания об одном типе феноменов для понимания другого, а поиск новых способов смотреть на вещи – это один из самых важных ментальных процессов, основанных на здравом смысле.




