Но как найти подобную функцию? Тут могут подойти многие уравнения. Вероятно, проще всего модифицировать линейную мальтузианскую модель: хnext = rх (1 – x). И снова величина r – коэффициент роста, который можно увеличить или уменьшить. Новый член (1 – x) удерживает рост в определенных границах, поскольку увеличение x приводит к уменьшению (1 – x)
[107]. Имея калькулятор, можно задать начальное значение, выбрать коэффициент роста и вычислить результат – численность популяции в следующем году.
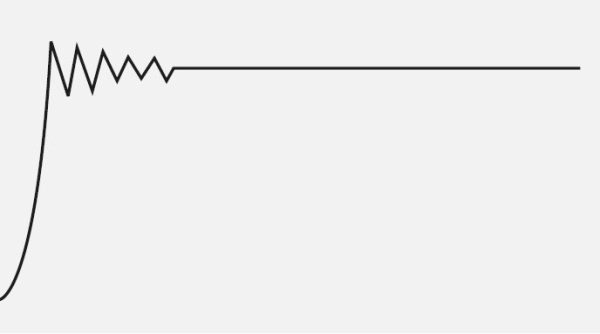
Популяция достигает равновесия после роста, чрезмерного увеличения численности особей и его снижения.
К 1950-м годам некоторые экологи уже использовали варианты рассмотренного выше уравнения, известного как логистическое разностное уравнение
[108]. В частности, Уильям Эдвин Рикер из Австралии применил его для оценки реальных рыбных промыслов. Ученые поняли, что коэффициент роста r является важной характеристикой модели. В физических системах, откуда, собственно, и были позаимствованы подобные уравнения, данный параметр отвечал количеству теплоты, или силе трения, или еще какой-нибудь непонятной величине, воплощающей нелинейность. Применительно к пруду с рыбами он должен соответствовать плодовитости рыб, способности популяции расти и вымирать (так называемому репродуктивному потенциалу). Вопрос заключался в том, как именно этот параметр влияет на дальнейшую судьбу изменяющейся популяции. Очевидно, что небольшое значение параметра повлечет за собой стабилизацию числа особей на относительно невысоком уровне, а значение побольше – на относительно высоком. Это справедливо для многих значений, но не для всех. Время от времени исследователи, и Рикер в их числе, наверняка использовали слишком большие значения – и должны были увидеть хаос.
Когда числа начинают странно себя вести, они доставляют человеку, вооруженному механической счетной машинкой с ручным приводом, изрядные неприятности. Конечно, числа не растут до бесконечности, но они и не сходятся к какому-то пределу. Впрочем, ни один из экологов 1960-х годов, по всей видимости, не был склонен (а может, им не хватало упорства) долго возиться с числами, которые отказываются к чему-либо сходиться. Так или иначе, колебания численности популяции давали экологам повод предположить, что происходят они вокруг некоего скрытого уровня равновесия. Считая последнее весьма важным, экологи даже не предполагали, что никакого равновесия может и не быть.
Справочники и учебники, посвященные логистическим уравнениям и их более сложным вариантам, не содержали, как правило, никаких указаний на возможные проявления неупорядоченности
[109]. Джон Мэйнард Смит в классической работе «Математические идеи в биологии», вышедшей в 1968 году, так определил возможные перспективы развития: численность популяции часто является величиной почти постоянной или колеблется вокруг предполагаемого положения равновесия «с весьма регулярной периодичностью». Автор не был столь наивен, чтобы допускать отсутствие неупорядоченного поведения в жизни реальных популяций. Он лишь полагал, что с описанными им математическими моделями такое поведение не имеет ничего общего. Будь это иначе, биологи избегали бы пользоваться подобными моделями. Если модель не оправдывала ожиданий своего создателя относительно реального положения дел в популяции, расхождение всегда можно было объяснить тем, что какая-то величина (возрастной состав популяции, специфика ареала или географической среды, соотношение полов) осталась неучтенной.
Но что важнее всего, в глубине души экологи всегда были склонны списывать неупорядоченность числового ряда на несовершенство счетной машинки или недостаточную точность таких вычислений
[110]. Интерес представляли устойчивые решения, порядок казался лучшей наградой. В конце концов, процедура подбора нужных уравнений и их решения требовала известных усилий. Никто не хотел впустую тратить время на ошибочные изыскания, не выявлявшие стойкой тенденции, и ни один опытный эколог не забывал, что его уравнения не более чем примитивная версия реальных явлений. На упрощения шли ради моделирования упорядоченности. Стоило ли преодолевать трудности, чтобы узреть хаос?
Позже скажут, что Лоренца сделал известным Джеймс Йорк и он же дал науке о хаосе ее нынешнее имя. Вторая часть этого утверждения справедлива.
Йорк был математиком, но предпочитал считать себя философом, хотя это и таило в себе некоторую опасность. Остроумный и велеречивый, всегда слегка лохматый, он обожал такого же всегда слегка лохматого Стива Смейла. Подобно многим, Йорк признавал, что понять Смейла непросто. Однако в отличие от большинства коллег он знал, почему же так трудно постичь логику Стива. Когда Йорку было двадцать два, он поступил в Физико-технологический институт при Мэрилендском университете (а позже его и возглавил). Он относился к числу тех математиков, которые во что бы то ни стало стремятся претворить свои идеи в жизнь, чтобы те принесли пользу. Написанный им доклад о распространении гонореи убедил федеральные власти в необходимости изменить стратегию контроля заболеваемости
[111]. Во время топливного кризиса 1970-х годов он выступил в суде штата Мэриленд с весьма корректными (но не слишком убедительными) аргументами в пользу того, что ограничение продаж бензина лишь усугубит ситуацию
[112]. Когда в эпоху антивоенных выступлений правительство опубликовало сделанные с самолета-шпиона фотографии – редкие группки людей вокруг монумента Вашингтону в разгар акции протеста, – Йорк проанализировал фотографию и по форме тени, отбрасываемой монументом, установил, что в действительности снимок был сделан на полчаса позже, когда митингующие уже расходились
[113].



