Странный аттрактор обитает в фазовом пространстве – одном из удивительнейших изобретений современной науки. Фазовое пространство делает возможным превращение чисел в изображения, извлекая малейшую существенную информацию из движущихся систем, механических или жидкостных, и наглядно демонстрируя все их возможности. Физики уже имели дело с двумя простыми типами «аттракторов» – фиксированными точками и замкнутыми кривыми, описывающими поведение таких систем, которые достигли устойчивого состояния или непрерывно себя повторяют.
В фазовом пространстве все известные данные о динамической системе в каждый момент времени концентрируются в одной точке, которая и представляет собой данную систему в конкретное мгновение. В следующее мгновение система уже претерпит изменения, пусть даже совсем незначительные, и точка изменит свое местонахождение. Всю историю существования системы можно изобразить на графике, отслеживая, как точка движется по своей орбите в фазовом пространстве с течением времени.
Но как же все данные о сложнейшей системе могут быть представлены лишь одной точкой? Если система характеризуется двумя переменными, найти ответ не составляет труда, он напрямую вытекает из декартовой геометрии, преподаваемой в средней школе: одна из переменных располагается на горизонтальной оси х, а другая – на вертикальной оси у. Если же система представляет собой качающийся маятник, свободный от действия силы трения, то одна из переменных является его положением в пространстве, а другая – скоростью. Они непрерывно меняются, образуя линию из точек, которая изгибается петлей, вновь и вновь повторяющей саму себя. Та же система, но обладающая более высокой энергией, раскачивающаяся быстрее и сильнее, образует в фазовом пространстве петлю, схожую с первой, но бо́льшую по размерам.
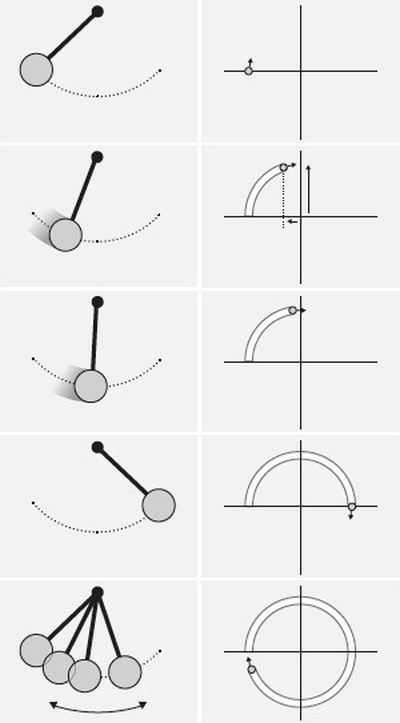
Новый способ изучения маятника. Единственная точка в фазовом пространстве (справа)передает всю информацию о состоянии динамической системы в конкретный момент времени (слева). Для простого маятника достаточно двух чисел, представляющих его скорость и местоположение. В момент начала колебательных движений маятника его скорость равна нулю, а местоположение выражается отрицательным числом, поскольку маятник находится слева от центра (верхний ряд). Два числа определяют положение одной точки в двумерном фазовом пространстве (второй ряд). Скорость достигает максимума, когда маятник минует самую нижнюю точку (третий ряд). Скорость вновь снижается до нуля, а затем меняет знак при движении влево (четвертый ряд).
Впрочем, столкнувшись с одним из проявлений реальности – трением, – система начинает претерпевать изменения. Чтобы описать судьбу маятника, подверженного трению, не нужны уравнения движения: каждая его орбита должна заканчиваться в одном и том же месте – в центре фазового пространства, где и местоположение, и скорость равны нулю. Эта центральная фиксированная точка как бы притягивает колебания. Вместо того чтобы вечно чертить на графике петли, орбита маятника спиралью закручивается внутрь. Трение рассеивает энергию системы, что в фазовом пространстве выглядит как толчок к центру. Наблюдается движение из внешних зон с высокой энергией к внутренним зонам с низкой энергией. Аттрактор – простейший из возможных – подобен магниту величиной с булавочную головку, встроенному в лист резины.
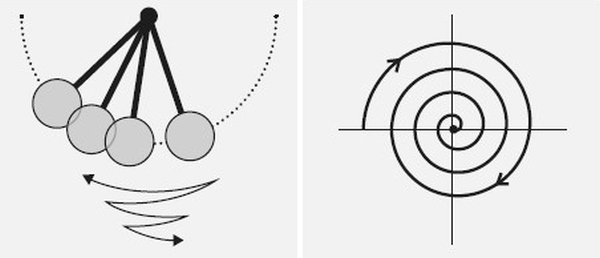
Точки образуют траекторию, которая позволяет наглядно представить непрерывное поведение динамической системы в течение длительного периода времени. Повторяющаяся «петля» соответствует системе, которая всегда воспроизводит одно и то же свое состояние. Если повторяющееся поведение устойчиво, как у часов с маятником, система при незначительных помехах возвращается к прежней орбите движения. В фазовом пространстве траектории вблизи орбиты как бы вовлекаются в нее, а сама орбита является аттрактором. Аттрактор может являть собой одну-единственную точку (справа). В случае с маятником, непрерывно теряющим энергию на трение, все траектории имеют форму спирали, закручивающейся внутрь, по направлению к точке, в которой система устойчива, – в этом состоянии движения не наблюдается вообще.
Одним из преимуществ рассмотрения состояний системы как совокупности точек в пространстве является то, что в таком случае легче наблюдать происходящие изменения. Система, в которой переменные непрерывно увеличиваются и уменьшаются, превращается в движущуюся точку, похожую на муху, летающую по комнате. Если некоторые комбинации переменных никогда не возникают, ученый может просто представить, что эта часть комнаты находится вне зоны досягаемости и насекомое никогда туда не залетит. При периодическом поведении изучаемой системы, когда она снова и снова возвращается к одному и тому же состоянию, траектория полета мухи образует петлю и насекомое минует одну и ту же точку в пространстве множество раз. Своеобразные портреты физических систем в фазовом пространстве демонстрировали образцы движения, которые были недоступны наблюдению иным способом. Так фотография природного ландшафта в инфракрасных лучах открывает те мелочи и детали, которые существуют вне досягаемости нашего восприятия. При взгляде на фазовую картину ученый мог, призвав на помощь воображение, уяснить сущность самой системы: петля здесь соответствует периодичности там, конкретный изгиб воплощает определенное изменение, а пустота говорит о физической невероятности.
Даже при наличии двух измерений изображения в фазовом пространстве могли многим удивить. Кое-какие из них можно было построить в том числе на мониторах настольных компьютеров, превращая уравнения в красочные траектории. Некоторые физики начали создавать серии движущихся картинок и снимать на видеопленку, чтобы продемонстрировать их своим коллегам. Математики из Калифорнии публиковали книги, иллюстрированные множеством красно-сине-зеленых рисунков в стиле анимации, – «комиксы хаоса», как отзывались о них, не без яда, коллеги авторов
[202]. Но пара измерений не охватывала всего богатства систем, которые хотели изучать физики, и ученые стремились ввести больше двух переменных, что, естественно, требовало увеличения числа измерений. Каждый фрагмент динамической системы, способный к независимому перемещению, является уже новой переменной, воплощая иную степень свободы, и для каждой такой степени требуется новое измерение в фазовом пространстве. Иначе нет уверенности, что одна-единственная точка содержит достаточно информации для описания состояния системы в каждый конкретный момент времени. Простые уравнения, изучавшиеся Робертом Мэем, задействовали одно измерение. Они позволяли обойтись единственным числом – значением температуры или численности популяции, – которое определяло местоположение точки на прямой, располагавшейся в одном измерении. Урезанная система Лоренца, описывавшая конвекцию в жидкостях, имела три фазовые координаты, но не потому, что жидкость двигалась в трех пространственных измерениях, а потому, что для описания состояния жидкости в каждый момент времени требовалось три вполне определенных числа.




