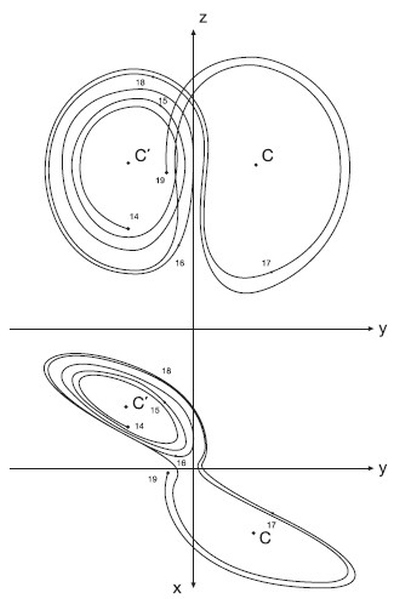
Первый странный аттрактор. В 1963 году Эдвард Лоренц смог вычислить только первые несколько петель аттрактора для своей простой системы уравнений. Однако он понял, что переплетение двух спиралеобразных «крыльев» должно иметь необычную структуру на бесконечно малых масштабах.
Аттрактор был устойчивым, непериодическим и имел малое число измерений. Он никогда не пересекал сам себя. Если бы подобное случилось и он возвратился бы в точку, которую уже миновал, движение в дальнейшем повторялось бы, образуя периодическую петлю. Но такого не происходило. В этом-то и заключалась странная прелесть аттрактора: являвшиеся взору петли и спирали казались бесконечно глубокими, никогда до конца не соединявшимися и не пересекавшимися. Тем не менее они оставались внутри участка пространства, ограниченного рамками параллелепипеда. Как такое стало возможным? Как может бесконечное множество траекторий лежать в ограниченном пространстве?
До того как изображения фракталов Мандельброта буквально наводнили научный мир, представить особенности построений подобных форм казалось весьма трудным. Сам Лоренц признавал, что в его собственном экспериментальном описании присутствовало «кажущееся противоречие». «Очень непросто слить две поверхности, если каждая содержит спираль и траектории не стыкуются», – сетовал ученый
[208]. Однако в массе компьютерных вычислений он все же разглядел слабо просматривавшееся решение. Лоренц понял, что, когда спирали начинали сходиться, поверхности должны были разделяться, образуя отдельные слои на манер теста в слоеном пирожном. «Мы видим, что каждая поверхность состоит на самом деле из двух, так что, когда они сходятся, поверхностей становится уже четыре. Проследив за аналогичным процессом с другой петлей, мы замечаем, что теперь поверхностей уже восемь, и так далее. В итоге мы можем заключить, что налицо бесконечное множество поверхностей, каждая из которых находится чрезвычайно близко к одной из двух изначально сходящихся поверхностей». Неудивительно, что в 1963 году метеорологи оставили подобные рассуждения без внимания. Десятилетие спустя Рюэль, узнав о труде Лоренца, был ошеломлен и взбудоражен. Впоследствии он посетил Лоренца, однако вынес из той встречи чувство легкого разочарования
[209]. Общие научные интересы исследователи обсуждали совсем недолго; с характерной для него робостью Лоренц постарался придать визиту светский характер: ученые с женами посетили художественный музей.
Пытаясь отыскать ключи к решению загадки, Рюэль и Такенс пошли двумя путями. Одним стала попытка дать теоретическое обоснование странным аттракторам. Являлся ли аттрактор Лоренца типичным? Возможны ли какие-то иные формы? Вторым путем, по которому пошли ученые, была экспериментальная деятельность. Она преследовала цель подтвердить или опровергнуть весьма далекое от математики убеждение, что странные аттракторы применимы к хаосу в природе.
В Японии, исследуя электронные схемы, имитировавшие колебание механических струн, но в ускоренном темпе, Ёсисукэ Уэда обнаружил последовательности невероятно прекрасных странных аттракторов. (И ему пришлось получить восточную версию прохладного отклика коллег, с которым в свое время столкнулся Рюэль: «Ваш результат есть не что иное, как вариант периодических колебаний. Нет никакой нужды разводить собственную концепцию устойчивых состояний»
[210].) В Германии Отто Рёсслер, непрактикующий доктор медицины, пришедший к исследованию хаоса через химию и теоретическую биологию, предпринял необычную попытку, отодвинув математику на второй план, взглянуть на странные аттракторы сквозь призму философии. Его именем стали называть один из простейших аттракторов – узкую ленту со сгибом, которую изучали довольно широко в силу легкости ее построения. Однако ученый облек в зримую форму и аттракторы с большим числом измерений. «Представьте сосиску, внутри которой заключена другая сосиска, а внутри нее еще одна, и еще, – говорил он. – Выньте ее, сверните, сожмите и положите обратно»
[211]. Действительно, сгибание и сжатие пространства оказались ключом к построению странных аттракторов и, возможно, даже к динамике порождавших их реальных систем. Рёсслер чувствовал, что эти формы олицетворяли принцип самоорганизации окружающего мира. Его воображению рисовалось нечто вроде ветроуказателя на аэродроме. «Закрытый с одного конца рукав с отверстием на другом конце, куда рвется ветер, – так описывал это исследователь. – Вдруг ветер оказался в ловушке. Его энергия, вопреки желанию, совершает нечто продуктивное, подобно дьяволу в средневековой истории. Принцип таков: природа делает что-то против своей воли и, запутавшись сама в себе, рождает красоту».
Создание изображений странных аттракторов вряд ли можно назвать обычным делом. Запутанные пути орбит вьются сквозь три и более измерений, образуя в пространстве темный клубок с внутренней структурой, невидимой извне. Чтобы представить подобную трехмерную «паутину» в виде плоских картин, ученые сначала применяли технику проекции. Рисунок являл собой тень, отбрасываемую аттрактором на поверхность. Однако странные аттракторы довольно сложны, так что проекция смазывает все детали и взору предстает путаница, которую почти невозможно расшифровать. Более эффективная техника заключается в построении так называемого отображения первого возвращения, или отображения Пуанкаре. Суть ее сводится к отделению «ломтика» запутанной сердцевины аттрактора и перенесению его в двумерное пространство, подобно тому как патологоанатом помещает срез ткани на предметное стекло микроскопа.
Отображение Пуанкаре лишает аттрактор одного измерения и превращает непрерывную линию в совокупность точек. Сводя аттрактор к отображению Пуанкаре, ученый по умолчанию считает, что сохранит самую суть движения. Он может вообразить, к примеру, что странный аттрактор вьется у него перед глазами, словно пчела, и его орбиты перемещаются вверх и вниз, влево и вправо, ближе и дальше от экрана компьютера – и каждый раз, когда орбита аттрактора пересекает плоскость экрана, она оставляет светящуюся точку в месте пересечения. Такие точки либо образуют похожее на кляксу пятно произвольной формы, либо начинают вычерчивать некий контур на экране.



