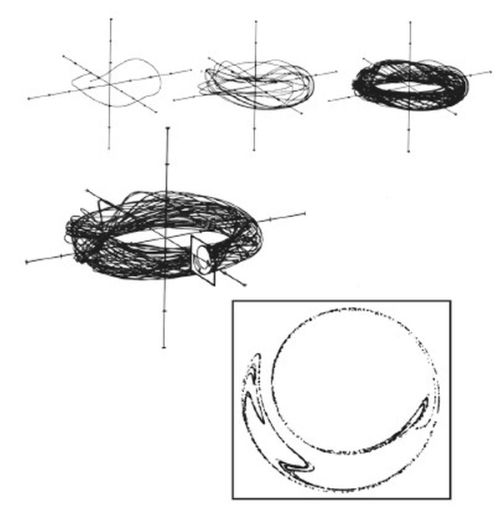
Структура аттрактора. Странный аттрактор, изображенный в верхнем ряду (сначала представлена одна орбита, затем десять и сто), иллюстрирует хаотичное поведение ротора – маятника, совершающего полный круг и регулярно приводимого в движение притоком энергии. Через некоторое время, когда на рисунке появится тысяча орбит (ниже), аттрактор превратится в запутанный клубок. Чтобы можно было исследовать его внутреннее строение, компьютер делает поперечный срез аттрактора – так называемое сечение Пуанкаре (рисунок в рамке). Этот прием уменьшает число измерений с трех до двух. Каждый раз, когда траектория пересекает плоскость, она оставляет на ней точку. Постепенно возникает весьма детализированный образ. Показанный здесь пример состоит более чем из восьми тысяч точек, каждая из которых соответствует целой орбите, окружающей аттрактор. Фактически «отбираются пробы» системы через равные промежутки времени. Одни данные утрачиваются, зато другие выявляются во всей своей выпуклости.
Описанный выше процесс соответствует «отбору образцов» состояния системы, который ведется не постоянно, а лишь время от времени. В какой момент брать пробу, то есть из какой области странного аттрактора вырезать ломтик, – дело исследователя. Временной интервал, в котором содержится наибольшее количество информации, должен соответствовать некоему физическому свойству динамической системы. Например, отображение Пуанкаре может отражать скорость отвеса маятника каждый раз, когда тот проходит низшую точку. Или экспериментатор волен выбрать определенный регулярный промежуток времени, «замораживая» последовательные состояния во вспышках воображаемого света, исходящего от стробоскопа. В любом случае в получаемых изображениях в конце концов проявится изящная фрактальная структура, о которой догадывался Эдвард Лоренц.
Наиболее доступный для понимания и самый простой странный аттрактор был построен человеком, весьма далеким от загадок турбулентности и гидродинамики, – астрономом Мишелем Эно из обсерватории Ниццы на южном побережье Франции
[212]. Бесспорно, в каком-то отношении астрономия дала толчок изучению динамических систем. Планеты, двигающиеся с точностью часового механизма, обеспечили триумф Ньютона и вдохновили Лапласа. Однако небесная механика значительно отличалась от земной: земные системы, теряющие энергию на трение, являются диссипативными, чего нельзя сказать об астрономических системах, считающихся консервативными, или гамильтоновыми. На самом деле в масштабе, близком к бесконечно малому, даже в астрономических системах наблюдается нечто вроде торможения. Оно происходит, когда звезды излучают энергию, а приливное трение несколько истощает кинетическую энергию движущихся по орбитам небесных тел. Однако для удобства в вычислениях астрономы пренебрегают рассеиванием, а без него фазовое пространство не будет складываться и сжиматься так, чтобы образовалось бесконечное множество фрактальных слоев. Странный аттрактор возникнуть не может. А может ли возникнуть хаос?
Не один астроном сделал карьеру, обойдя стороной динамические системы, но не таков был Эно. Он родился в Париже в 1931 году, всего на несколько лет позже Лоренца, и тоже представлял собой тот тип ученого, которого неумолимо влечет к математике. Ему нравилось решать небольшие конкретные вопросы, которые могли быть привязаны к определенным физическим проблемам, – по его собственному выражению, «не то, что делают современные математики». Когда компьютеры стали доступны даже любителям, подобная машина модели Heathkitпоявилась и у Эно. Собрав ее собственноручно, ученый наслаждался компьютерными забавами. Кстати, задолго до описываемых событий он исследовал особенно сложную проблему из области динамики. Она касалась шаровых звездных скоплений, в которых число светил доходит до миллиона. Это древнейшие и, возможно, наиболее интересные объекты ночного неба. Плотность их вызывает изумление. Как такое огромное количество звезд сосуществует в ограниченном объеме пространства и эволюционирует во времени, астрономы пытались выяснить в течение всего XX века.
С точки зрения динамики, моделирование шарового звездного скопления представляет собой «задачу многих тел». Задача двух тел очень простая, Ньютон ее полностью решил: каждое из пары тел, например Земля и Луна, описывает идеальный эллипс вокруг общего центра тяжести системы. Но добавьте хотя бы еще один обладающий тяготением объект – и все изменится. Задача трех тел уже более чем трудна – как показал Пуанкаре, в большинстве случаев она неразрешима. Можно просчитать орбиты для некоторого временно́го интервала, а с помощью мощных вычислительных машин их удается отследить и в течение более длительного периода, но потом возникают помехи. Эти уравнения не решаются аналитически, то есть долгосрочный прогноз поведения системы из трех тел сделать невозможно. Устойчива ли Солнечная система?
[213] Конечно, если рассматривать ее в короткой перспективе, она выглядит устойчивой, но даже сегодня никто не уверен в том, что орбиты некоторых планет не перестанут быть гелиоцентрическими, заставив небесные тела навсегда покинуть Солнечную систему.
Система вроде шарового звездного скопления слишком запутанна, чтобы исследовать ее «в лоб», как задачу многих тел. Однако динамику скопления можно изучить, прибегнув к некоторым хитростям. Вполне допустимо, в частности, рассматривать единичные звезды, путешествующие в пространстве, в некотором усредненном гравитационном поле с определенным центром тяготения. Однако время от времени две звезды будут подходить друг к другу настолько близко, что их взаимодействие нужно будет рассматривать отдельно. Астрономы поняли, что шаровые скопления вообще не должны быть устойчивыми: внутри них обычно образуются так называемые бинарные звездные системы, в которых звезды парами перемещаются по небольшим компактным орбитам. Когда с подобной системой встречается третья звезда, одна из трех, как правило, получает резкий толчок. Со временем энергия, полученная ею благодаря такому взаимодействию, достигнет уровня, достаточного для того, чтобы звезда набрала скорость, позволяющую вырваться из скопления. Таким образом одно из тел покидает систему, а пространство скопления после этого слегка сжимается. Когда в 1960 году в Париже Эно выбрал эту задачу темой своей диссертации, он произвольно предположил, что шаровое звездное скопление, изменив свой масштаб, останется самоподобным. Произведя расчеты, ученый получил потрясающий результат: ядро скопления «сплющится», приобретая кинетическую энергию и стремясь к бесконечно плотному состоянию. Подобное трудно было вообразить. Да и данные исследования скоплений, полученные к тому времени, не подтверждали этот вывод. Однако теория Эно, впоследствии названная гравотермальным коллапсом, постепенно овладевала умами ученых.
Ободренный результатом и готовый к неожиданностям, весьма вероятным в научной работе, астроном занялся более легкими вопросами динамики звезд. Он попытался применить математический подход к давно существующим проблемам.



