Человек, ищущий в беспорядочной информации скрытые формы, должен проделать один и тот же опыт десятки и сотни раз, прежде чем начнут проясняться закономерности в поведении крошечной ячейки. Когда Либхабер и его помощник постепенно увеличивали температуру и система переходила от одного состояния равновесия к другому, порой наблюдались весьма специфичные явления. Иногда появлялись промежуточные частоты, плавно скользившие по спектральной диаграмме и вскоре исчезавшие. Иногда изменялась наблюдаемая геометрия – и вместо двух валиков жидкости появлялось три. И как в такой ситуации понять, что же на самом деле происходит внутри маленькой стальной ячейки?
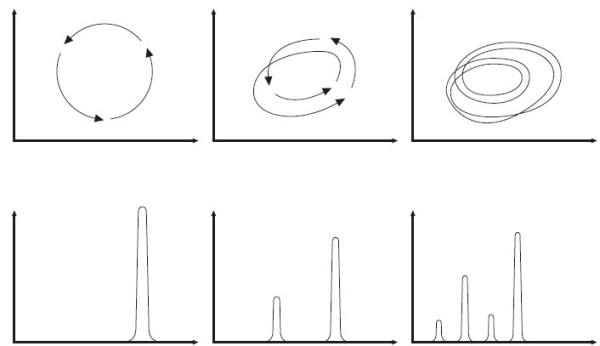
Два способа наблюдения бифуркаций. Когда в опыте, подобном тому, который поставил Либхабер, наблюдаются устойчивые колебания, их образ в фазовом пространстве представляет собой петлю, повторяющую саму себя через равные промежутки времени (вверху слева). Экспериментатор, строящий спектральную диаграмму, увидит тогда один высокий пик для данной частоты (внизу слева). После бифуркации удвоения периода система уже дважды образует петлю, прежде чем повторит сама себя (вверху в центре), а ученый видит еще и новый пик, соответствующий половине прежней частоты, или удвоенному прежнему периоду (внизу в центре). Новые удвоения периодов наделяют спектральную диаграмму все большим и большим числом пиков (справа).
Знай тогда Либхабер об открытии Фейгенбаумом универсальности, он бы точно представлял, где искать нужные бифуркации и как их называть. К 1979 году все больше математиков и сведущих в математике физиков обращали внимание на новую теорию Фейгенбаума, но в массе своей ученые, знакомые с трудностями изучения реальных физических систем, считали, что у них есть веские основания воздерживаться от каких-либо определенных суждений на сей счет. В одномерных системах вроде тех, которые исследовали Мэй и Фейгенбаум, сложность – это одно, но в двух-, трех– или четырехмерных системах реальных механизмов, конструируемых инженерами, – совсем другое. Для ее описания требуются не просто разностные, а громоздкие дифференциальные уравнения. Более того, еще одна пропасть отделяла низкоразмерные системы от систем жидкостных потоков, которые физики рассматривали как системы с потенциально бесконечным числом измерений. Даже ячейка Либхабера, столь искусно сработанная, содержала, по сути, несметное число частиц жидкости, и каждая из них обладала как минимум возможностью двигаться независимо. А значит, при определенных обстоятельствах любая частица могла стать источником нового изгиба или вихря.
«Никто и не помышлял, что нужное нам основное движение в подобной системе упрощается и описывается отображениями», – признался Пьер Хоэнберг из лабораторий AT amp;T Bellв Нью-Джерси
[273]. Он входил в число тех немногих физиков, которые доверяли как новой теории, так и связанным с ней экспериментам. «Фейгенбаум, может быть, и мечтал о таком, но не высказывал своих мечтаний вслух. Его работа была посвящена отображениям. Почему они должны интересовать физиков? Забава, не более того… Пока шли игры с отображениями, все казалось слишком далеким от того, что мы действительно стремились понять. Но когда теория подтвердилась на практике, она нас не на шутку взволновала. Самое удивительное заключается в том, что, исследуя по-настоящему интересные системы, все равно можно в деталях понять их поведение при помощи модели с малым числом степеней свободы».
В конце концов, именно Хоэнберг познакомил экспериментатора и теоретика. Летом 1979 года он организовал семинар в Аспене, на котором побывал и Либхабер. (Четырьмя годами ранее, на такой же летней встрече, Фейгенбаум слушал доклад Стива Смейла о числе – всего лишь числе, – которое возникло, когда математик наблюдал переход к хаосу в определенном уравнении.) Когда Либхабер описал свои опыты с жидким гелием, Хоэнберг взял их на заметку. По пути домой он заглянул в Нью-Мексико повидаться с Фейгенбаумом. Вскоре после этого Фейгенбаум посетил Либхабера в Париже. Ученые стояли посреди беспорядочно разбросанных деталей и инструментов в лаборатории Либхабера, и тот с гордостью продемонстрировал свою миниатюрную ячейку, дав Фейгенбауму возможность разъяснить последний вариант своей теории
[274]. Затем они вместе бродили по Парижу в поисках хорошей кофейни, и позже Либхабер вспоминал, как был удивлен, увидев столь молодого и, как он выразился, «живого» ученого-теоретика.
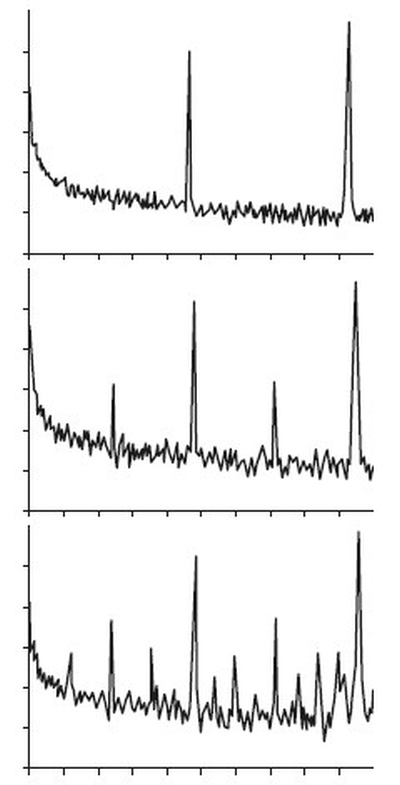
Реальные данные, подтверждающие теорию. Спектральные диаграммы Либхабера наглядно показали точный рисунок удвоения периодов, ранее предсказанный теоретически. Всплески новых частот отчетливо выделялись на фоне экспериментальных шумов. Теория масштабирования Фейгенбаума предсказывала не только когда и где появятся новые частоты, но также и насколько высокими будут пики.
Переход от отображений к реальным потокам жидкости казался настолько значительным достижением, что даже самые щепетильные ученые восприняли его как чудо. Каким образом природа смогла сочетать крайнюю сложность с предельной простотой, не понимал никто. Джерри Голлаб предложил «рассматривать это не как обычную связь между теорией и опытом, а как некое волшебство»
[275]. И это волшебство в течение нескольких лет повторялось снова и снова в огромном бестиарии лабораторных систем: в увеличенных в размерах ячейках с водой и ртутью, электронных осцилляторах, лазерах и даже в химических реакциях
[276]. Теоретики, восприняв методы Фейгенбаума, обнаружили и иные математические пути к хаосу, родственные удвоению периодов, – перемежаемость и квазипериодичность, которые тоже доказали свою универсальность как в теории, так и в опытах.
Открытия ученых помогли начаться эре компьютерных экспериментов. Физики обнаружили, что вычислительные машины воспроизводят изображения, аналогичные тем, что наблюдаются в реальных опытах, только в миллионы раз быстрее и куда надежнее. Многим еще более убедительной, нежели результаты Либхабера, казалась жидкостная модель Вальтера Франческини из Университета Модены (Италия) – система из пяти дифференциальных уравнений, генерировавшая аттракторы и удвоение периодов
[277]. Хотя Франческини ничего не знал о Фейгенбауме, его сложная модель с большим числом измерений выдавала те же постоянные, которые Фейгенбаум вычислил с помощью своих одномерных отображений. В 1980 году группа европейских ученых выработала довольно убедительное математическое объяснение феномена: диссипация «опорожняет» сложную систему, устраняя множество противодействующих движений и фактически преобразуя поведение множества измерений в одно
[278].




