Когда Хаббард запустил компьютер, намереваясь более детально исследовать пространство, начала вырисовываться картина, которая сбила с толку и преподавателя, и его студентов. Например, вместо аккуратного «гребня» между синей и красной долинами математик увидел пятна зеленого цвета, соединенные словно бусины ожерелья. Это выглядело так, будто шарик, попавший в ловушку на стыке двух соседних долин, остановился в третьей, самой отдаленной. Граница между двумя цветами никогда не формировалась полностью, и при увеличении линия между зеленым пятном и синей областью включала в себя вкрапления красного цвета
[287]. И так повторялось снова и снова. Линия границы в конце концов открыла Хаббарду особое свойство, которое показалось бы весьма странным даже человеку, знакомому с жуткими фракталами Мандельброта: ни одна из точек не разделяет только два цвета. Где бы два цвета ни старались соединиться, там всегда появляется третий, порождая целые ряды самоподобных проникновений. Непостижимо, но каждую пограничную точку окаймляли зоны всех трех цветов.

Бесконечно сложные границы. Когда пирог разделен на три части, все эти части соприкасаются разом только в одной точке, а границы между любыми двумя из них выглядят простыми. Но многие процессы в абстрактной математике и физике реального мира создают невообразимо сложные границы. На представленном слева вверху рисунке метод Ньютона, примененный для нахождения кубического корня из −1, делит плоскость на три равные части, одна из которых закрашена белым. Все белые точки «притягиваются» к корню, лежащему в самой большой белой части; все черные точки «притягиваются» к одному из двух других корней. У границы есть особое свойство: каждая точка на ней граничит со всеми тремя частями. И, как показывают рисунки справа и внизу, при увеличении фрагменты этой границы обнаруживают фрактальную структуру, повторяющую основной рисунок во все меньшем и меньшем масштабе.
Хаббард начал изучать обнаруженные сложные формы и обдумывать значение этого открытия для математики. В результате его работа, а также исследования коллег ознаменовали собой новую попытку разрешить проблемы динамических систем. Ученому стало ясно, что изображения, построенные с помощью метода Ньютона, принадлежат целому семейству еще не открытых изображений, отражающих действия сил в реальном мире. Майкл Барнсли столкнулся с другими фрагментами такого же рода, а Бенуа Мандельброт, как вскоре поняли и Хаббард, и Барнсли, обнаружил прародителя всех этих форм.
Множество Мандельброта, как любят повторять его почитатели, является наиболее сложным объектом во всей математике
[288]. Чтобы увидеть его полностью – круги, усыпанные колючими шипами, спирали и нити, завивающиеся наружу и кругом, с выпуклыми пестрыми молекулами, висящими, словно виноградины на личной лозе Господа Бога, – не хватит и вечности. Если разглядывать это множество в цвете на подходящем экране, оно кажется более фрактальным, нежели сами фракталы, настолько оно сложно устроено при любом масштабировании. Построение каталога различных составляющих элементов или числовое описание очертаний этого множества потребует бесконечного количества данных. Однако, как это ни парадоксально, для передачи по линии связи его полного описания хватит нескольких десятков строчек кода: в короткой компьютерной программе содержится достаточно информации, чтобы воспроизвести все множество целиком. Догадавшиеся первыми, каким образом в нем смешиваются сложность и простота, были застигнуты врасплох – как и сам Мандельброт. Для широкой публики множество Мандельброта превратилось в эмблему хаоса. Оно замелькало на глянцевых обложках сборников тезисов конференций и инженерных ежеквартальных журналов и сделалось украшением выставки компьютерного искусства, показанной во многих странах в 1985–1986 годах. Его красота ощущалась сразу. Гораздо труднее было уловить математический смысл. Ученые долго вникали в его суть.
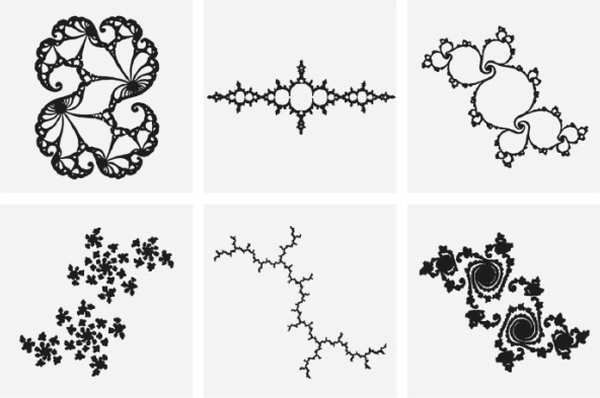
Много различных фрактальных изображений можно получить с помощью итераций в комплексной плоскости, но множество Мандельброта – единственное и неповторимое. Смутное и призрачное, оно начало вырисовываться, когда ученый попытался сделать какие-то общие выводы о классе фигур, известных как множества Жюлиа. Множества эти были открыты и изучены еще во время Первой мировой войны французскими математиками Гастоном Жюлиа и Пьером Фату, работавшими без каких бы то ни было компьютерных изображений. Мандельброт познакомился с их скромными рисунками и прочитал их работу, уже канувшую в безвестность, когда ему было двадцать лет. Именно множества Жюлиа во всем разнообразии обличий оказались тем, что поставило в тупик Барнсли. Некоторые из множеств Жюлиа похожи на круги, проколотые и деформированные во многих местах, что придает им фрактальную структуру, другие разбиты на зоны, а некоторые представляют собой россыпь пылинок. Для их описания не подходят ни обычные слова, ни понятия евклидовой геометрии. Французский математик Адриан Дуади заметил: «Получив непредсказуемо многоликие образы множеств Жюлиа, мы видим, что одни выглядят словно пухлое облако, другие представляют собой тощий куст ежевики, третьи похожи на искорки, плывущие в воздухе после фейерверка. Один объект напоминает кролика, и многие имеют хвосты, как у морских коньков»
[289].
В 1979 году Мандельброт понял, что может создать в пределах комплексной плоскости один образ, который послужит своего рода каталогом множеств Жюлиа, ориентиром для каждого из них
[290]. Тогда он изучал итерационные решения квадратных и тригонометрических уравнений (последние включали функции синуса и косинуса). Даже построив всю свою интеллектуальную карьеру вокруг гипотезы, что простота порождает сложность, он отнюдь не сразу осознал, насколько необычным был объект, возникший на экранах его компьютеров в IBM и Гарварде. Он пытался добиться от программистов большей детальности изображения, и они бросили силы на то, чтобы эффективно перераспределить загруженную память и получить новые интерполяции точек на машине IBM с ее черно-белым дисплеем низкого разрешения. Вдобавок ко всему им приходилось следить за тем, чтобы не попасть в известную компьютерщикам ловушку артефактов, возникающих из-за сбоя в работе машины и исчезающих при изменении программы, что еще больше осложняло дело.