Бо́льшая часть моего описания касалась систем циркуляции, но те же самые принципы действуют и в отношении дыхательных систем, деревьев и других растений, насекомых и клеток. Собственно говоря, тот факт, что один и тот же набор принципов устройства сетей порождает в системах с весьма разными сложившимися в процессе эволюции конструкциями сходные законы масштабирования, является крупным успехом этой теории. Эти принципы не только объясняют происхождение вездесущего в разных таксономических группах степенного масштабирования с четвертными показателями, но и показывают, например, почему аорты масштабируются так же, как стволы деревьев. Теория позволяет вычислить многие такие величины, и некоторые из них представлены в приведенных ниже таблицах, взятых из наших собственных статей, опубликованных в журналах Science и Nature, чтобы проиллюстрировать ее предсказательную силу. Мы сравниваем предсказанные значения самых разных величин, касающихся кровеносных и дыхательных систем, растений и лесных систем, с результатами наблюдений. Легко видеть, что в большинстве случаев наблюдается превосходное согласие.
Таблица 1. Сердечно-сосудистая система
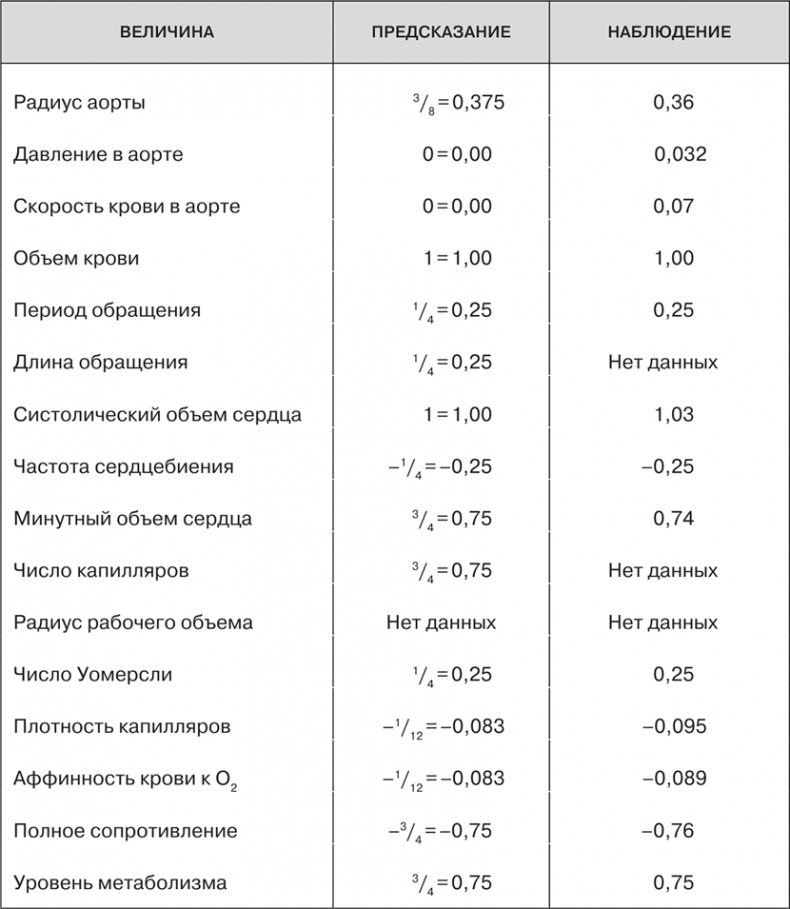
Таблица 2. Дыхательная система
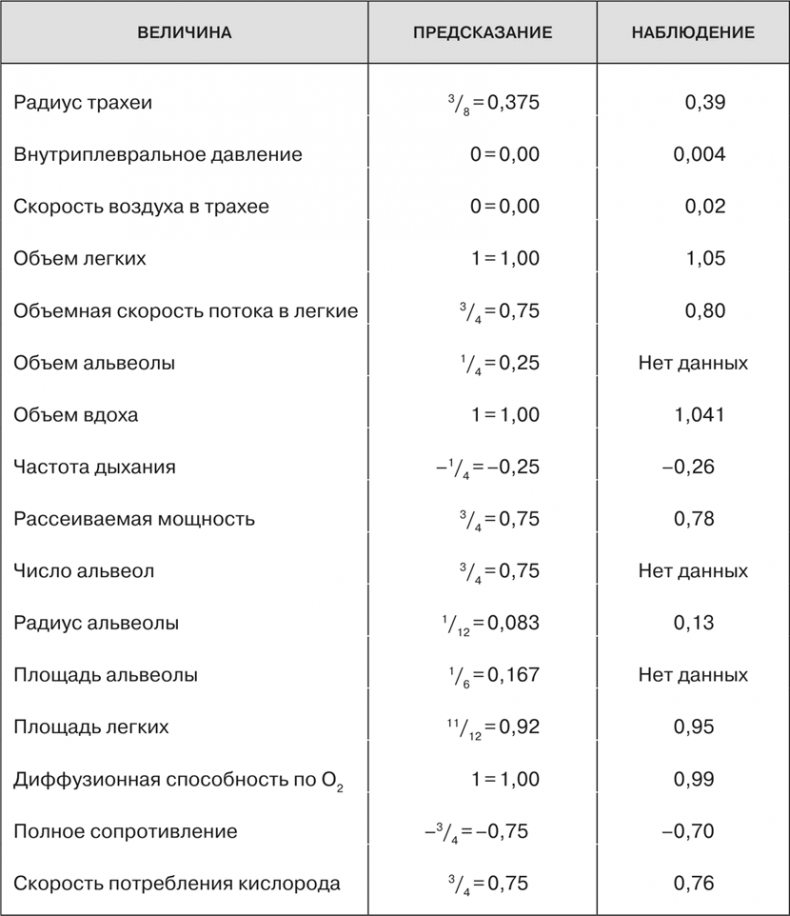
Таблица 3. Предсказанные значения показателей масштабирования для физиологических и анатомических переменных сосудистой системы растений
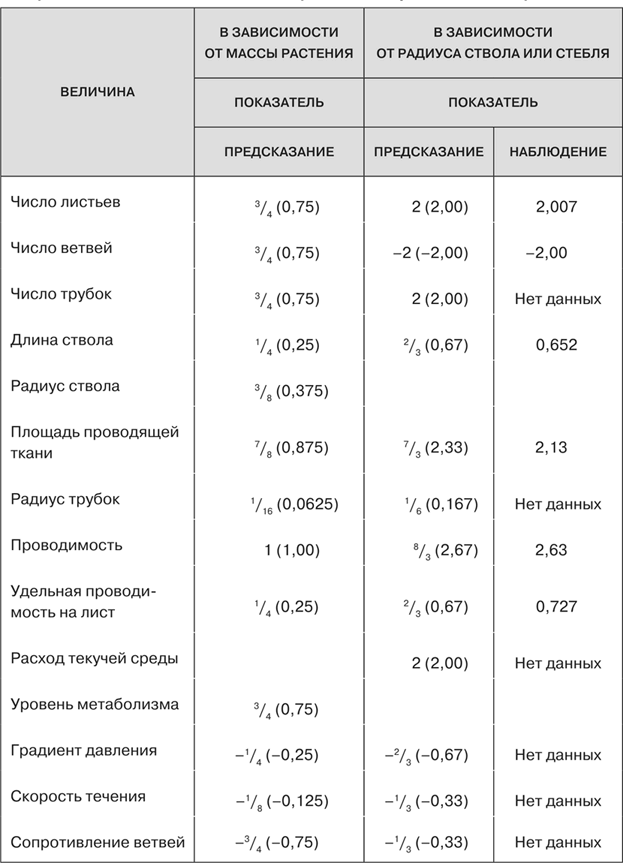
Несмотря на то что в основе всегда лежит один и тот же набор принципов, конкретные математические описания и динамические картины в каждом случае обычно бывают весьма разными, что отражает разные физические структуры сетей. Я не стану углубляться в подробности того, как одни и те же принципы применяются во всех этих различных системах, но во всех случаях получаются очень близкие результаты и проявляется степенное масштабирование с четвертными показателями.
Все это очень приятно, но не дает ответа на один навязчивый вопрос: почему во всех этих, очень разных, сетях возникает именно степенной показатель ¼? Почему в одной сети он не может быть равен, скажем, 1/6, в другой – 1/8 и так далее? Другими словами, чем обусловлен тот факт, что применение этого одинакового для всех набора правил к разным сетевым системам с самыми разными структурами и динамическими особенностями дает одни и те же показатели степенных законов масштабирования? Существуют ли какие-то дополнительные конструктивные принципы, не зависящие от динамики конкретных систем, которые обеспечивают возникновение этой четверти практически во всех группах организмов? Этот вопрос имеет большое концептуальное значение, особенно для понимания причин, по которым такое всеобщее поведение охватывает даже такие системы, как бактерии, для которых выявить явную, иерархически разветвленную сетевую структуру гораздо труднее.
1. Четвертое измерение жизни
Общее рассуждение при рассмотрении этого вопроса может быть основано на том утверждении, что естественный отбор привел не только к минимизации потерь энергии, но и к максимизации метаболической способности, так как именно метаболизм производит энергетические и материальные ресурсы, необходимые для поддержания и воспроизводства жизни
[74]. Для этого была максимизирована площадь поверхностей, через которые эти ресурсы передаются. Эти поверхности составляют на самом деле суммарную площадь поверхности всех концевых модулей сети. Например, вся наша метаболическая энергия передается для питания наших клеток через суммарную площадь поверхности всех капилляров, а метаболизм деревьев определяется передачей энергии, извлеченной из солнечного света всеми его листьями для обеспечения процесса фотосинтеза, и воды, собираемой из почвы всеми концевыми волокнами корневой системы. Таким образом, концевые модули важны не только по причине своей неизменности, но и потому, что они обеспечивают взаимодействие с поставляющей ресурсы средой, они могут быть и внутренними, как в случае капилляров, и внешними, как в случае листьев. Как мы увидим в дальнейшем, эта центральная роль шлюза для обмена энергией принципиально важна для многих аспектов жизни, от определения длительности сна до определения продолжительности жизни.
Естественный отбор использовал фрактальную природу заполняющих пространство сетей для максимизации суммарной эффективной поверхности этих концевых модулей и тем самым максимизации интенсивности метаболизма. С геометрической точки зрения вложенные уровни постоянного ветвления и извилистости, присущие фракталоподобным структурам, оптимизируют передачу информации, энергии и материалов путем максимизации площади поверхности, через которую протекают эти необходимые для жизни элементы. Благодаря своей фрактальной природе эти поверхности гораздо больше, чем их кажущиеся физические размеры. Проиллюстрируем это положение несколькими замечательными примерами, взятыми из нашего собственного тела.
Хотя размер наших легких приблизительно равен размеру футбольного мяча, имеющего объем порядка 5–6 л, суммарная площадь поверхности альвеол, то есть концевых модулей дыхательной системы, в которых происходит обмен углекислого газа и кислорода с кровью, почти равна площади теннисного корта, а суммарная длина всех воздушных каналов составляет около 2500 км, что почти равно расстоянию от Лос-Анджелеса до Чикаго или от Лондона до Москвы. Еще поразительнее тот факт, что длина всех артерий, вен и капилляров человеческого тела, выложенных в одну линию, составила бы около 100 000 км, что почти в 2,5 раза больше окружности Земли и превышает треть расстояния до Луны… И все это умещается в нашем теле высотой от полутора до двух метров. Несмотря на всю свою фантастичность, это лишь одно из удивительных свойств нашего тела, результата использования естественным отбором чудес физики, химии и математики.
Это замечательное явление – предельное проявление того же принципа, который Ричардсон открыл, а Мандельброт сформулировал в приложении к береговым линиям и границам, а именно что длины и площади – не всегда то, чем они кажутся. Как было объяснено в предыдущей главе, достаточно морщинистая линия, заполняющая пространство, может масштабироваться так, как будто она – поверхность. Ее фрактальность, по сути дела, придает ей дополнительное измерение. Ее обычная евклидова размерность, обсуждавшаяся в главе 2, по-прежнему остается равной 1, что говорит о том, что это именно линия, но ее фрактальная размерность равна 2, что свидетельствует о ее максимальной фрактальности и о том, что ее длина масштабируется как площадь. Точно так же и поверхность, если она достаточно измята, может вести себя как объемное тело, там самым приобретая дополнительное измерение. Ее евклидова размерность равна 2, поскольку это поверхность, но ее фрактальная размерность равна 3.





