1. Масштабирование городов
Одним из первых к нашей работе присоединился Дирк Хелбинг; когда я познакомился с ним, он был директором Института транспорта и экономики Дрезденского технологического университета в Германии. Дирк получил образование в области статистической физики и применял ее методы к изучению дорожного движения и толп пешеходов. Сейчас он работает в престижной Швейцарской высшей технической школе Цюриха, обычно называемой аббревиатурой ЕТН, в которой он руководит крупным проектом под названием «Модель живой Земли» (Living Earth Simulator). Эта система должна моделировать при помощи больших массивов данных и замысловатых алгоритмов глобальные явления, от экономических систем, правительств и культурных тенденций до эпидемий, сельского хозяйства и технического прогресса.
В 2004 г. Дирк поручил одному из своих студентов, Кристиану Кунерту, исследовать, как изменяются различные характеристики европейских городов в зависимости от их размеров. Некоторые из результатов этих ранних исследований представлены на рис. 33, и из них ясно видно, что данные по разным странам и городам демонстрируют удивительную простоту и регулярность
[116]. Эти графики отражают, возможно, одну из самых прозаических характеристик городов, а именно зависимость числа заправочных станций от размеров города. Число заправок отложено по вертикальной оси, а размеры города, измеренные по численности его населения, – по горизонтальной оси. Как и на предыдущих графиках, иллюстрировавших явления масштабирования, здесь использован логарифмический масштаб, то есть величины, отложенные по осям, последовательно увеличиваются на степени десяти. Даже если не знать никакой математики, не помнить, что такое логарифм, и не очень разбираться в городах, ясно видно, что число заправочных станций изменяется в зависимости от размеров города с удивительной регулярностью. Данные не рассеяны беспорядочным образом по всему графику, а с хорошей точностью ложатся на простую прямую линию, что ясно указывает на то, что эта зависимость не произвольна, а соответствует четко определенному системному поведению. Получающаяся прямая линия говорит о том, что число заправочных станций возрастает с увеличением численности населения в соответствии с простым степенным законом, очень напоминающим то, что мы наблюдали ранее в масштабировании биологических и физических величин.
Более того, наклон этой прямой, соответствующий показателю степенного закона, составляет около 0,85, что чуть выше, чем значение 0,75 (знаменитые ¾), которое мы видели в масштабировании уровня метаболизма организмов (рис. 1). Не менее интересно и то, что этот показатель остается приблизительно одинаковым для масштабирования числа заправок во всех странах, представленных на графиках. Его значение, приблизительно равное 0,85, меньше 1, так что, используя введенную выше терминологию, можно сказать, что это масштабирование сублинейно, что говорит о наличии систематической экономии на масштабе. Другими словами, чем больше город, тем меньше заправочных станций требуется на душу его населения. Таким образом, каждая заправочная станция в большом городе в среднем обслуживает больше клиентов и продает в месяц больше топлива, чем в городе меньших размеров. Точнее говоря, при каждом удвоении численности населения городу требуется приблизительно на 85 % больше заправочных станций – а не в два раза больше, как можно было бы наивно предполагать, – что дает порядка 15 % экономии при каждом удвоении размеров. Этот эффект может стать весьма значительным, если сравнить, например, маленький город с населением порядка пятидесяти тысяч с мегаполисом, население которого в сто раз больше, около пяти миллионов человек. Для обслуживания стократно большего населения требуется всего лишь в пятьдесят раз больше заправок, так что в подушном исчислении такому большому городу их нужно в два раза меньше, чем маленькому.
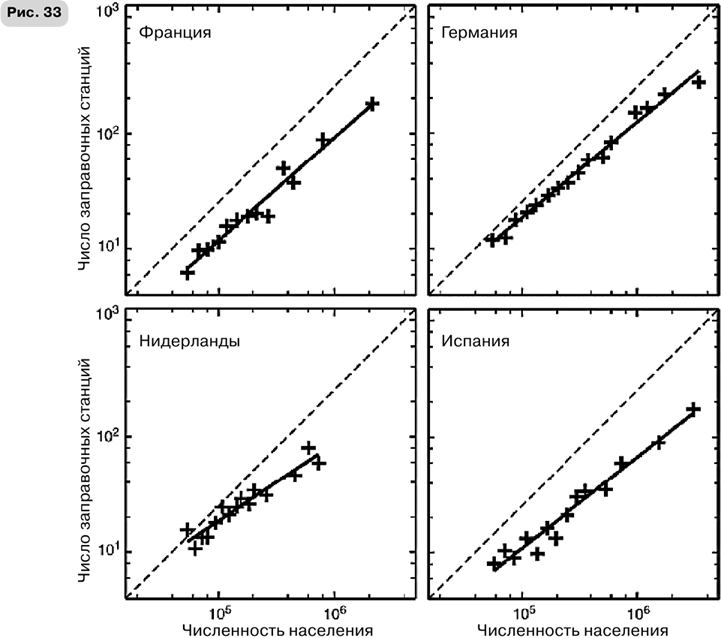
Зависимости числа заправочных станций от размеров городов четырех европейских стран, представленные в логарифмическом масштабе, свидетельствуют о сублинейном масштабировании с близкими показателями. Штриховая линия имеет наклон, равный 1, и соответствует линейному масштабированию
То, что в больших городах требуется меньшее число заправок на душу населения, чем в малых, может быть, и не столь удивительно. Удивительно то, что эта экономия на масштабе оказывается настолько систематической: она приблизительно одинакова для всех стран и везде подчиняется одному и тому же математическому закону масштабирования с показателем около 0,85. Еще удивительнее то, что другие инфраструктурные величины, связанные с сетями транспорта и снабжения, – суммарная длина линий электропередачи, дорог, водопроводов и газопроводов – масштабируются очень похожим образом с приблизительно такими же показателями, то есть близкими к 0,85. Более того, это систематическое поведение, по-видимому, остается неизменным во всех точках мира, для которых удалось получить соответствующие данные. То есть в отношении инфраструктуры города ведут себя в точности как организмы: они подчиняются простым степенным законам сублинейного масштабирования, что обеспечивает систематическую экономию на масштабе, хотя и меньшую, что отражает разница между степенными показателями (для организмов он равен 0,75, а для городов – 0,85).
Распространение этой изначальной попытки исследования на вопрос о масштабировании городов по более широкому спектру параметров и в большем числе стран было осуществлено чрезвычайно талантливой группой новых участников проекта. Среди них был Луис Беттанкур, с которым я познакомился, когда он, защитив диссертацию по астрофизике, изучал в Лос-Аламосе ранние этапы эволюции Вселенной. После этого он провел пару лет в MIT, а затем вернулся в Лос-Аламос на постоянную должность в группе прикладной математики. Хотя Луис родился, вырос и получил образование в Португалии, это было совершенно незаметно: он говорит по-английски настолько бегло и без какого-либо иностранного акцента, что когда я впервые встретился с ним, то принял его за англичанина. Собственно говоря, свою диссертацию по физике он защитил именно в Имперском колледже Лондона, на математическом факультете которого по случайному совпадению работаю я. Языковым талантам Луиса вполне соответствуют и его научные таланты. Он очень быстро включился в проект изучения городов и занялся сбором и анализом данных со всего мира. Он стал страстным приверженцем дела углубленного изучения городов и приобрел репутацию одного из лучших в мире специалистов в этой области.
В этом предприятии к Луису присоединился еще один блестящий новичок, Хосе Лобо, специалист по городской экономике, работающий сейчас в программе устойчивости в Университете штата Аризона. Когда мы с ним познакомились, Хосе был молодым преподавателем факультета городского и регионального планирования Корнеллского университета и уже в течение нескольких лет приезжал в SFI. Как и Луис, Хосе вложил в нашу программу свой немалый талант в области статистики и сложного анализа данных, а кроме того, привнес в нее свои профессиональные знания в сфере устройства городов и урбанизации, которые оказались жизненно важными для нашей совместной работы.



