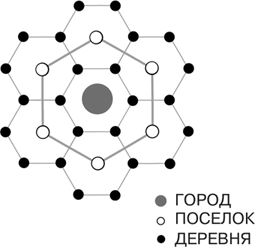
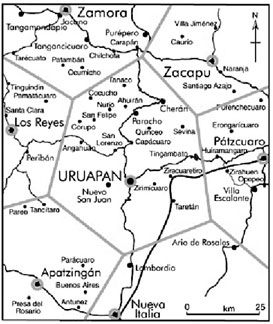
Концепция гексагональной решетки центральных мест Кристаллера и подтверждающие его идею «данные реального мира» из центральной области Мексики
Теория Кристаллера курьезным образом созвучна его имени: он утверждал, что городские системы, а следовательно, и отдельные города можно представить в виде идеализированных двумерных структур кристаллической геометрии, построенных на основе высокосимметричного рисунка гексагональной решетки, повторяющегося на все меньшем и меньшем масштабе. Пример такой решетки приведен на иллюстрации. Шестиугольники были выбраны потому, что это простейшие геометрические фигуры, которые можно расположить встык так, чтобы полностью покрыть географическую область города или городской системы без каких-либо пробелов. Эти шестиугольники играют роль «центральных мест» торговли, причем внутри них заключены шестиугольные центральные места меньшего размера. На эту схему Кристаллера навели его наблюдения, согласно которым в Южной Германии мелкие города сходных размеров расположены приблизительно на одинаковых расстояниях друг от друга (и предположительно образуют вершины шестиугольника), а более крупные, центральные города играют роль узловых точек (расположенных в центрах шестиугольников). Хотя такой регулярности обычно и не наблюдается в большинстве городских систем или внутри самих городов, предложенная Кристаллером модель геометрии городских систем обладает двумя очень важными качествами, общими с сетевыми системами, образовавшимися органически. Речь идет о свойствах заполнения пространства и самоподобия (и, следовательно, иерархичности), хотя оба этих термина появились лишь впоследствии. В его модели были и другие важные особенности, например идея минимизации по времени и расстоянию пути до места получения услуг, к которой мы еще вернемся.
Несмотря на то что недостатки теории центральных мест хорошо известны, она остается важным идеологическим компонентом современного планирования и проектирования городов. В начале 1950-х она легла в основу преобразования муниципальных отношений и границ во вновь созданной Федеративной Республике Германии (то есть Западной Германии), и эта система сохранилась до сих пор. Довольно парадоксальным образом после Второй мировой войны Кристаллер вступил в Коммунистическую партию, хотя во время войны он работал на СС и был членом НСДАП. Основываясь на своей теории, он разработал грандиозный план преобразования экономической географии завоеванных в ходе расширения Германии территорий Чехословакии и Польши. Еще одно, на сей раз трагическое, проявление иронии судьбы в этой истории заключается в том, что немецкий экономист Август Лёш, которого считают основоположником дисциплины региональных исследований, более всего известный расширением теории Кристаллера и приданием ей менее статичного, более математического и более реалистичного характера, был активным участником протестантского движения, резко выступавшего против нацизма. Во время войны он остался в Германии и скрывался, но умер от скарлатины через несколько дней после ее окончания. Ему было всего лишь тридцать девять лет.
Реально существующее самоподобие городов лучше отражает органически развившиеся сетевые структуры транспортных и коммунальных систем, чем жесткие гексагональные кристаллические схемы Кристаллера. Город – это не искусственная машина, спроектированная «сверху вниз» с преобладанием прямых линий и классической евклидовой геометрии; он гораздо ближе к организмам с их извилистыми линиями и фрактальными формами, характерными для сложных адаптивных систем – одной из которых он и является. Это ясно видно даже при беглом взгляде на типичный рисунок роста города: как показано на приведенных внизу снимках, непрерывное расширение филигранной сети его инфраструктуры напоминает рисунок роста колонии бактерий. Тщательный математический анализ таких рисунков подтверждает, что города – действительно самоподобные фракталы, весьма сходные с биологическими организмами или с береговыми линями в географии. Например, результаты измерений длины реальных границ города с разным разрешением, аналогичных тем, которые Льюис Фрай Ричардсон проводил для длины побережий, представленные в логарифмическом масштабе, дают прямые линии, наклон которых можно считать фрактальной размерностью границ города.

Слева: органический рост Парижа, демонстрирующий развитие фрактальной геометрии. Справа: развитие фрактальной геометрии в колонии бактерий
Как я уже объяснял выше, фрактальная размерность – это мера морщинистости объекта, и кое-кто интерпретирует ее как меру его сложности. На волне взрывного интереса к фракталам и вызванного им появления в 1980-х гг. теории сложности выдающийся урбанист Майкл Бэтти провел большое статистическое исследование городов, чтобы определить их фрактальные размерности
[120]. Бэтти и его сотрудники, а также другие исследователи, последовавшие их примеру, установили, что эти размерности составляют порядка 1,2, но могут сильно колебаться, доходя приблизительно до 1,8. Помимо того что фрактальная размерность представляет собой параметр, по которому можно сравнивать уровни сложности разных городов, возможно, самое интересное ее свойство состоит в том, что она служит своего рода барометром здоровья города. Фрактальная размерность здорового, жизнеспособного города обычно устойчиво увеличивается по мере его роста и развития, что отражает увеличение сложности по мере сооружения все большей и большей инфраструктуры для обслуживания растущего населения, занимающегося все более разнообразной и сложной деятельностью. Напротив, когда город переживает период экономических трудностей или временно уменьшается в размерах, его фрактальная размерность уменьшается.
Значения фрактальной размерности представляют собой меру самоподобия различных инфраструктурных сетей города; их определяют по результатам анализа схем, подобных представленным на предыдущей странице, с разным разрешением. Однако простого взгляда на физическую структуру города не всегда бывает достаточно для понимания его фрактальной природы. В конце концов, план улиц Нью-Йорка, да и почти любого другого американского города, обычно представляет собой регулярную прямоугольную сетку – практически ничего более простого и евклидова и не бывает. Это, очевидно, не относится к городам Старого Света, например, Лондону или Риму, извивающиеся улицы которых имеют более явную фрактальную органическую структуру. Но во всех случаях, даже под геометрией городов с прямоугольными сетками улиц, скрывается фрактальность, свойственная всем городам и проявляющаяся в универсальности законов масштабирования.





