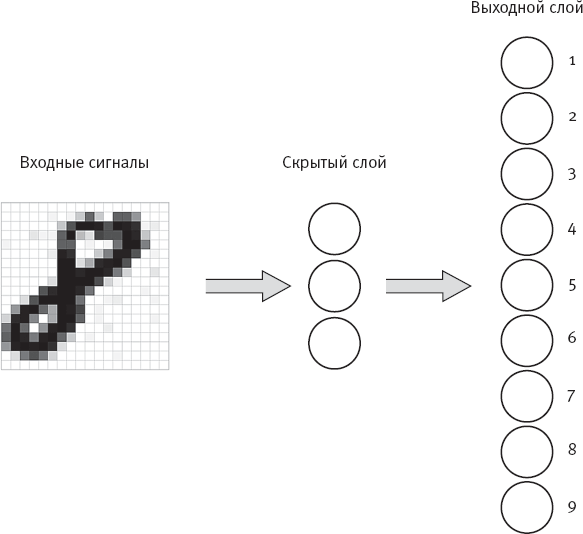
Рис. 4. Двухслойная нейронная сеть для распознавания рукописных цифр
Крупные серые стрелки показывают, что каждый входной сигнал имеет взвешенную связь с каждой скрытой ячейкой, а каждая скрытая ячейка имеет взвешенную связь с каждой выходной ячейкой. Загадочный термин “скрытая ячейка” позаимствован из литературы о нейронных сетях, им обозначается любая невыходная ячейка. Возможно, лучше было бы назвать ее “внутренней ячейкой”.
Представьте структуру вашего мозга, где некоторые нейроны непосредственно управляют “выходными сигналами”, например движением ваших мышц, но большинство нейронов просто взаимодействует с другими нейронами. Такие нейроны можно назвать скрытыми нейронами мозга.
Изображенная на рис. 4 сеть называется “многослойной”, поскольку имеет два слоя ячеек (скрытых и выходных) вместо одного слоя выходных сигналов. Теоретически многослойная сеть может иметь несколько слоев скрытых ячеек, и сети, имеющие более одного слоя скрытых ячеек, называются глубокими сетями. “Глубина” сети определяется количеством ее скрытых слоев. Я подробнее расскажу о глубоких сетях в последующих главах.
Подобно перцептронам, каждая ячейка здесь умножает каждый входной сигнал на вес связи этого входного сигнала, а затем суммирует результаты. В отличие от перцептрона, ячейка здесь не просто “выдает сигнал” или “не выдает сигнал” (то есть выдает 1 или 0) в зависимости от порогового значения, а использует полученную сумму, чтобы вычислить число между 0 и 1, которое называется “активацией” единицы. Если единица получает маленькую сумму, ее активация близка к 0, а если сумма большая, активация близка к 1. (Для интересующихся я описала некоторые математические подробности в примечании
[41].)
Чтобы обработать такое изображение, как рукописная восьмерка с рис. 4, сеть проводит вычисления слой за слоем, слева направо. Каждая скрытая ячейка вычисляет свое значение активации, затем эти значения активации становятся входными сигналами для выходных ячеек, которые вычисляют собственную активацию. В сети с рис. 4 активацию выходной единицы можно считать степенью уверенности сети в том, что она “видит” соответствующую цифру, а категорию цифры с самой высокой степенью уверенности – ответом сети, или классификацией.
Теоретически многослойная нейронная сеть может научиться использовать свои скрытые ячейки так, чтобы распознавать более абстрактные характеристики (например, визуальные формы, такие как верхний и нижний “кружки” рукописной восьмерки) вместо простых характеристик (например, пикселей), закодированных во входном сигнале. Как правило, заранее сложно понять, сколько скрытых слоев и сколько скрытых ячеек в каждом слое необходимо, чтобы сеть хорошо справлялась с поставленной задачей. Большинство исследователей нейронных сетей находит оптимальные настройки методом проб и ошибок.
Обучение методом обратного распространения ошибки
В книге “Перцептроны” Минский и Пейперт усомнились в возможности создания успешного алгоритма для определения весов в многослойной нейронной сети. Во многом именно из-за их скепсиса (и сомнений других специалистов из лагеря символического ИИ) финансирование исследований нейронных сетей в 1970-х резко сократилось. Однако, несмотря на негативный эффект книги Минского и Пейперта, небольшой костяк исследователей нейронных сетей продолжил работу, особенно в сфере когнитивной психологии Фрэнка Розенблатта. К концу 1970-х и началу 1980-х годов некоторые исследовательские группы явным образом опровергли предположения Минского и Пейперта о “бесплодности” многослойных нейронных сетей, разработав для них общий алгоритм обучения – метод обратного распространения ошибки для тренировки этих сетей.
Как следует из названия, метод обратного распространения ошибки состоит в том, чтобы взять ошибку, наблюдаемую в выходных ячейках (например, высокую степень уверенности в неверной цифре у сети на рис. 4) и “распространить” вину за эту ошибку в обратном порядке (на рис. 4 в направлении справа налево), распределив вину по ячейкам сети. Таким образом метод обратного распространения ошибки определяет, в какой степени нужно скорректировать каждый из весов для снижения погрешности. В ходе обучения нейронные сети просто постепенно корректируют веса связей так, чтобы погрешность каждого выходного сигнала на всех тренировочных примерах оказалась как можно ближе к 0. Хотя математика метода обратного распространения ошибки выходит за рамки моего рассказа, я описала некоторые тонкости в примечании
[42].
Метод обратного распространения ошибки будет работать (по крайней мере теоретически) вне зависимости от того, сколько в вашей нейронной сети входных сигналов, скрытых ячеек и выходных ячеек. Хотя нет математической гарантии, что метод обратного распространения ошибки остановится на верных весах для сети, на практике он прекрасно справляется со многими задачами, которые слишком сложны для простых перцептронов. Так, я натренировала и перцептрон, и двухслойную нейронную сеть, имеющие по 324 входных сигнала и 10 выходных сигналов, распознавать рукописные цифры, применив шестьдесят тысяч примеров, а затем протестировала каждую из систем на десяти тысячах новых примеров. Перцептрон выдавал верный ответ примерно в 80 % случаев, а нейронная сеть с 50 скрытыми ячейками верно распознала целых 94 % новых примеров. Слава скрытым ячейкам! Но чему именно научилась нейронная сеть, чтобы обойти перцептрон? Я не знаю. Возможно, я могла бы найти способ визуализировать 16 700 весов
[43] нейронной сети, чтобы пролить свет на ее работу, но я этого не сделала. В целом людям непросто понять, как эти сети принимают решения.



