Программа Сэмюэла для игры в шашки была основана на анализе дерева игры – и такой анализ по-прежнему остается фундаментом всех программ для игры в настольные игры (включая AlphaGo, которую я опишу далее). На рис. 30 показано дерево игры в шашки. “Корнем” дерева (обычно он находится на схемах сверху, в отличие от корней настоящего дерева) служит исходное положение шашек на доске до совершения первого хода. От корня расходятся “ветки”, ведущие ко всем ходам, доступным первому игроку (здесь – черным). Возможных ходов семь (для простоты на рисунке показаны лишь три из них). Для каждого из семи возможных ходов черных есть семь возможных ответов белых (не все они показаны на рисунке) и так далее. На рис. 30 каждая доска показывает возможное положение шашек, называемое позицией на доске.
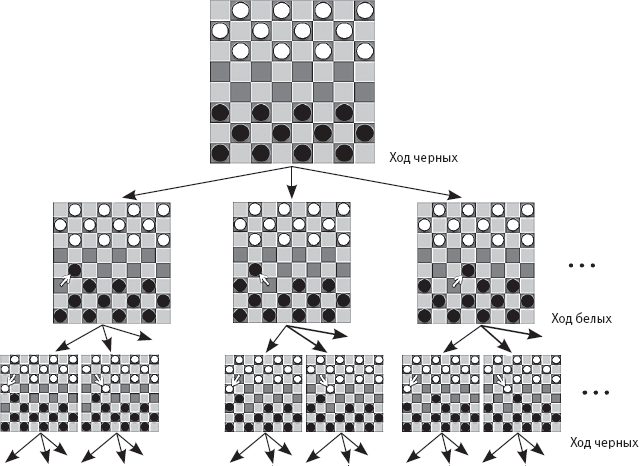
Рис. 30. Фрагмент дерева игры в шашки. Для простоты на рисунке показано всего по три возможных хода для каждой позиции на доске. Белыми стрелками показано передвижение шашки с предыдущей клетки на текущую
Представьте, что вы играете в шашки. Перед каждым ходом вы, возможно, строите в уме небольшой фрагмент этого дерева. Вы мыслите следующим образом: “Если я схожу вот так, то противник сможет сходить вот так, после чего я схожу вот так и возьму одну шашку”. Большинство людей, включая чемпионов игры, рассматривают лишь несколько возможных ходов, просчитывая лишь несколько шагов, прежде чем сделать ход. Быстрый компьютер, напротив, имеет возможность просчитывать игру гораздо дальше. Что мешает компьютеру рассмотреть все возможные ходы и определить, какая последовательность ходов ведет к победе быстрее всего? Проблема в экспоненциальном росте, пример которого мы видели в главе 3 (помните царя, мудреца и рисовые зерна?). В среднем за партию в шашки совершается около пятидесяти ходов, а это значит, что дерево игры с рис. 30 может иметь пятьдесят уровней. На каждом уровне каждая позиция на доске предполагает в среднем шесть или семь возможных ходов – следовательно, общее количество позиций в дереве может превышать шесть в пятидесятой степени, а это невероятно большое число. Гипотетическому компьютеру, который способен просматривать триллион позиций в секунду, понадобится более 1019 лет, чтобы рассмотреть все позиции единственного дерева игры. (Для наглядности это число можно сравнить с возрастом Вселенной, который составляет всего около 1010 лет.) Таким образом, полный анализ дерева игры не представляется возможным.
К счастью, для успешной игры компьютерам не нужно заниматься столь обстоятельным анализом. Обдумывая каждый ход, шашечная программа Сэмюэла создавала (в компьютерной памяти) небольшой фрагмент дерева игры, как на рис. 30. Корнем дерева служила текущая позиция на доске, и программа, используя встроенные знания правил шашек, генерировала все ходы, которые можно совершить из этой позиции. Затем она генерировала возможные ходы оппонента из каждой из итоговых позиций – и так далее, на четыре-пять ходов (“слоев”) вперед
[192].
Затем программа оценивала позиции в конце упреждающего просмотра – на рис. 30 это позиции на нижнем уровне фрагмента дерева игры. Оценка позиции на доске предполагает присвоение ей числового значения ценности, которая определяет, с какой вероятностью конкретная позиция приведет к победе программы в игре. Программа Сэмюэла использовала оценочную функцию, которая присваивала очки различным элементам позиции, таким как численное преимущество черных, количество черных дамок и количество черных шашек, близких к попаданию в дамки. Сэмюэл выбрал эти элементы на основе своих знаний о шашках. Когда каждая из позиций нижнего уровня получала такую оценку, программа применяла классический алгоритм максимин, который использовал значения ценности, присвоенные в конце упреждающего просмотра, чтобы оценить ходы, непосредственно доступные программе в текущей позиции. Затем программа выбирала ход, получивший наивысшую оценку.
Предполагается, что оценочная функция работает точнее при применении к позициям, которые могут возникнуть дальше по ходу игры, и потому программа сначала анализирует все возможные последовательности ходов на несколько шагов вперед, а затем применяет оценочную функцию к итоговым позициям на доске. Затем оценки распространяются обратно по дереву с помощью максимина, который оценивает все возможные ходы из текущей позиции
[193].
В процессе обучения программа узнавала, какие именно элементы позиции необходимо включать в оценочную функцию на каждом ходу, а также как взвешивать эти элементы при суммировании их оценок. Сэмюэл попробовал несколько методов обучения системы. В самом интересном варианте система училась, играя сама с собой! Этот метод обучения был довольно сложен, и я не стану описывать его в подробностях, но в некоторых аспектах он стал предтечей современного обучения с подкреплением
[194].
В итоге шашечная программа Сэмюэла добилась впечатляющих результатов, сравнимых с показателями игроков “выше среднего уровня”, но не чемпионов игры. Любители назвали программу “сложным, но победимым” соперником
[195]. Стоит отметить, что программа стала для IBM неожиданным подарком: на следующий день после того, как Сэмюэл представил ее на национальном телевидении в 1956 году, стоимость акций IBM взлетела на 15 %. Впоследствии компания еще несколько раз наблюдала подобное повышение стоимости акций после демонстрации игровой программы, побеждающей людей: не так давно стоимость акций IBM взлетела после привлекшего огромное количество зрителей выпуска телепрограммы Jeopardy!, в котором разработанная компанией программа Watson одержала победу над людьми.
Несомненно, шашечная программа Сэмюэла стала важной вехой в истории ИИ, но я устроила этот исторический экскурс в основном для того, чтобы на ее примере ввести три важнейших понятия: дерево игры, оценочная функция и обучение посредством игры с самим собой.
Deep Blue
Хотя “сложная, но победимая” шашечная программа Сэмюэла была выдающейся, особенно по тем временам, вряд ли можно сказать, что она заставила людей сомневаться в уникальности собственного разума. Даже если бы машина могла обыграть чемпионов по шашкам (как в итоге произошло в 1994 году
[196]), мастерство в шашках никогда не считалось признаком большого ума. С шахматами все иначе. По словам Демиса Хассабиса из DeepMind, “десятки лет ведущие специалисты по информатике полагали, что с учетом традиционного статуса шахмат как мерила человеческого интеллекта умелая шахматная компьютерная программа может превзойти человека и по всем остальным показателям”
[197]. Многие, включая пионеров ИИ Аллена Ньюэлла и Герберта Саймона, ставили шахматы на пьедестал. В 1958 году Ньюэлл и Саймон написали: “Если получится создать успешную шахматную машину, получится и проникнуть в самое сердце интеллектуальной деятельности человека”
[198].



