Разве это не замечательный ход мысли? Он позволяет увидеть за следами факты и, расшифровав язык геометрии, раскрыть истину. Тщательное изучение улик сочетается здесь с безупречным логическим анализом. Разве не в этом секрет триумфа гениального сыщика – и, в нашем случае, высшей математики?
Отношения Холмса с математикой вполне понятны – это его зеркальное отображение. Именно поэтому, когда Конан Дойлю хочется ввести в повествование антагониста, который станет противостоять наблюдательному сыщику, он придумывает математика профессора Мориарти. «Наполеон преступного мира» описывается как «гений, философ» и «абстрактный мыслитель», кроме того, он – «прославленный автор “Движения астероидов”, книги, затрагивающей такие высоты чистой математики, что, говорят, не нашлось никого, кто мог бы написать о ней критический отзыв»
[16].
Поневоле приходишь в уныние, стоит подумать, как быстро Мориарти разобрался бы в следах велосипеда. Соперник Холмса, можно быть уверенными, знал о касательных.

Я сам впервые узнал о загадке с велосипедом из прекрасной биографической книги «Гений играет: пытливый ум Джона Хортона Конвея» Шивон Робертс. В одной запоминающейся сцене команда из трех математиков собирается вести экспериментальный курс в Принстоне. Он представляет собой «подпольную, бунтарскую попытку», направленную на то, чтобы показать, что «математика и поэзия похожи», и называется «Геометрия и воображение». Ожидая, что на занятиях будет не более 20 студентов, преподаватели ошарашены, когда выясняется, что на курс записалось 92 человека. Как рассказывает Робертс, молодые люди не потратили свои деньги зря:
Преподаватели строго соблюдали ритуал и появлялись в классе все разом, иногда с большой помпой и важностью, порой они несли флаг, время от времени надевали велосипедные шлемы, часто тянули за собой детскую тележку, наполненную многогранниками, зеркалами, фонариками и свежими продуктами из продуктового магазина…
Для одного урока преподаватели «отыскали огромные рулоны бумаги, разорванные на полосы размером, по меньшей мере, 1,8 метра на 6 метров» и ездили по ним на велосипедах с вымазанными краской колесами. В результате получились эпические полотна геометрического велосипедного искусства, головоломки в натуральную величину. Студенты, как юные Шерлоки, получили задание определить, в каком направлении ехал каждый велосипедист.
Но преподаватели добавили деталь, которая, возможно, озадачила бы самого Мориарти:
Тем не менее часть из этих следов поставила студентов в тупик. Эту серию линий Питер Дойль [один из преподавателей] оставил на листе бумаги, когда ездил туда-обратно на велосипеде с одним колесом.

VII
Биография массового увлечения, у которой нет автора
Это история о том, как рождаются вирусные сенсации. Решайте сами, что это будет: может быть, хулахупы, кубики Рубика, тамагочи или дешевый вариант последних, который еще называют iPhone. Но это не обязательно должна быть игрушка! Вы можете выбрать лингвистику, технологию, социальную сеть, образование опухолей или популяцию кроликов. Что угодно, что бы ни пришло вам в голову и, как это обычно бывает с повальными увлечениями, что тут же хочется получить всем вокруг.
«Как, – спросите вы, плюясь от возмущения, – как одна глава может годиться на любой случай жизни, как вы можете предлагать каждому выбрать свое собственное приключение?»
Ну, потому что на самом деле это история кривой. Эта кривая:
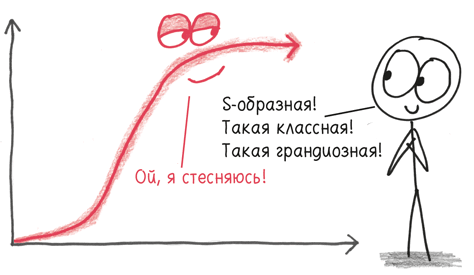
Эта основная модель, которая называется логистической кривой, – одна из величайших математических моделей, не говоря уж о том, что она является триумфом элементарного математического анализа. И, как и любая классическая пьеса, она разыгрывается в трех актах.
Акт I. Ускорение.
Когда мы что-то начинаем, наше увлечение еще не является модным веянием. Это всего лишь дикая прихоть. «Я буду продавать камень как питомца», – говорит какой-то сумасшедший. «Я поставлю танец с необычными движениями рук, и весь мир будет восторженно кричать: “Эй, макарена!”» Или даже: «Я введу в компьютер странички с фотографиями лиц и стану тем самым Цукербергом, Разрушителем миров».
Звучит как иллюзорная мечта? Возможно. Но вначале рост идет медленно.
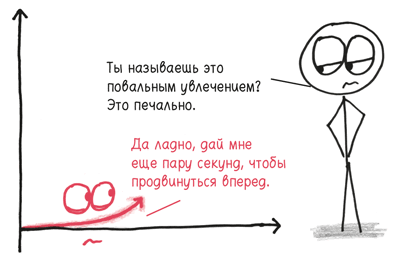
Но дела обстоят не так безрадостно, как кажется. Во время неблагоприятного начала рост на самом деле идет по экспоненте.
Слова «экспонента» или «экспоненциальный» проникли в обычный язык, как некоторые другие математические термины. («Внутреннее произведение» и «двудольный граф» все еще пребывают в трагическом забвении.) Тем не менее, как это всегда бывает, когда альтернативная рок-группа добивается успеха, по пути кое-что утрачивается. Об экспоненциальном росте обычно говорят как о синониме «очень быстрого», но его математическое значение гораздо более чудесно и точно: величина растет пропорционально своему размеру.
Другими словами, чем она больше, тем быстрее растет.

При линейном росте за каждый период времени прибавляется одно и то же количество. Это может происходить медленно, как прибавление одного кольца к стволу дерева каждый год. Или это может быть быстро, как рост мутантного дерева в сказке о Джеке и бобовом зернышке, когда каждое новое кольцо прибавлялось за миллисекунду. Важна не скорость, а постоянство. Если темп роста никогда не меняется, то он является линейным.
В противовес этому возьмем, к примеру, стартап, чья прибыль растет на 8 % каждый месяц. Поначалу 8 % от мизерного количества – это сущая безделица. Но со временем компания расширяется, и эти 8 % соответствуют все большим и большим цифрам. За девять месяцев доход удваивается, а за десять лет фирма превращается из гусеницы с выручкой в $1000 в месяц в огромную бабочку с прибылью в $8 млн в месяц. Дайте ей еще десять лет, и она станет громадиной с ежемесячным доходом в $1 трлн – 15 % мирового ВВП. Вот это и есть экспоненциальный рост.








