Вы можете уловить суть этого различия по двум коротким уравнениям:
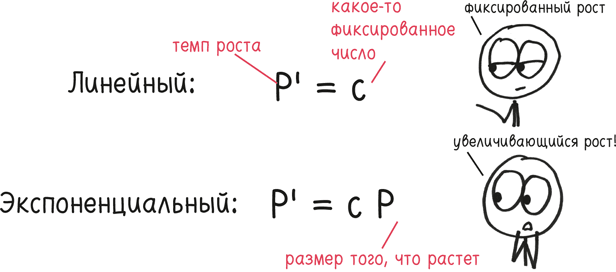
Но медовый месяц с экспонентой не может длиться вечно, иначе любое массовое увлечение захватило бы всю Вселенную. В реальности подобное пока что случалось только дважды: с крупяными куклами
[17] и деббингом
[18]. Немного времени спустя нас ждет акт II – Перегиб кривой.
Как и «экспоненциальный рост», выражение «точка перегиба кривой» перекочевало в обычный язык из учебников математики. Я сам всегда аплодирую вирусному распространению математического жаргона, но должен отметить, что фраза: «момент, когда рост неожиданно становится взрывным» – придает точке перегиба кривой почти противоположное значение.
При росте по логистической кривой перегиб происходит не в момент, когда начинается быстрый рост. Он происходит, когда быстрый рост доходит до кульминации, до своего максимума, и, таким образом, начинается долгое, медленное понижение.
Производная, как вы помните, говорит нам об изменениях графика. Положительная производная? Он растет. Отрицательная? Снижается.
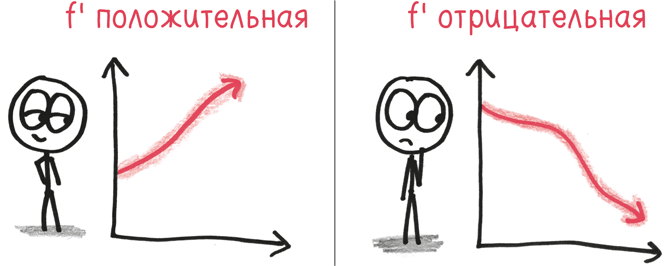
Вторая производная говорит нам о том, как меняется первая производная – то есть о самом темпе роста. Положительная вторая производная? Тогда наш рост ускоряется. Отрицательная вторая производная? Он замедляется.
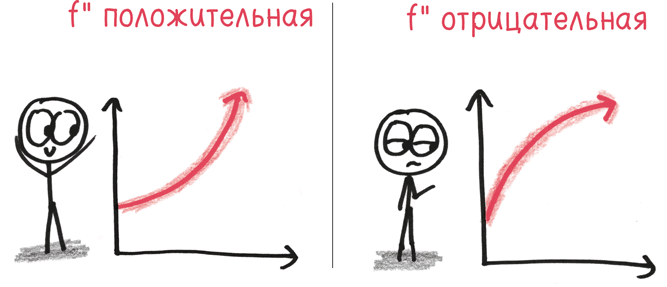
Точка перегиба кривой – это момент перехода, когда вторая производная меняет знак: отрицательный на положительный или (при росте по логистической кривой) положительный на отрицательный. После того как скорость растет и растет, как у потерявшего управление поезда или заигранного хита, ускорение, наконец, останавливается, и рост начинает замедляться.
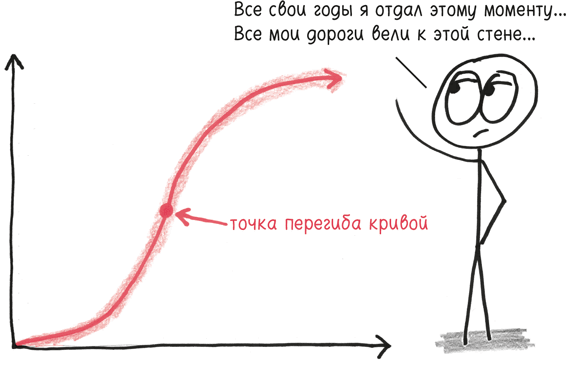
Это особый момент в истории массовых увлечений – триумф с привкусом горечи, поскольку все вершины достигнуты. В случае, скажем, с Instagram – это месяц, когда к нему присоединилось наибольшее количество пользователей. Социальная сеть еще не получила свое самое широкое распространение, но пик самого быстрого распространения пройден. Она расширялась быстрее, чем когда-либо ранее, и такого роста не будет уже никогда. Согласно графику то, что произойдет дальше, – это зеркальное отражение первоначальной траектории: каждому моменту ускорения теперь соответствует спад.
Это приводит нас к акту III – Насыщение.
В этот момент массовое увлечение перерастает свою крутизну. О нем знают родители. О нем знают даже бабушки и дедушки. Даже те, кто не в курсе модных тенденций популярной культуры – например, учителя математики, – могут решить присоединиться к стороне победителя. Чувство гордости первых адептов этого веяния сменяется теперь пренебрежением. Как подметил король парадокса Йоги Берра, «в этот ресторан больше никто никогда не ходит, потому что он всегда переполнен».
При экспоненциальной модели рост пропорционален размеру. Рост по логистической кривой добавляет еще один очень важный момент: рост пропорционален размеру, а также расстоянию от максимальной величины.
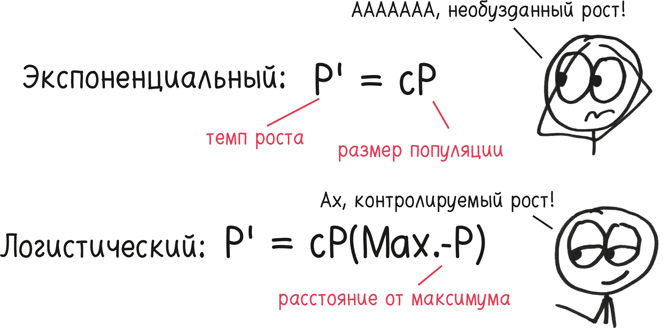
Чем ближе к максимуму, тем медленнее рост.
Лес может вместить только определенное количество кроликов, экономика – определенное количество электромобилей, человеческий глаз может выдержать только определенное количество просмотров «Gangnam Style». Ресурсы каждой системы конечны. Facebook никогда не сможет стать больше, чем население планеты, если только не снимет свой пагубный запрет заводить страницы дельфинам и гориллам.
В качестве иллюстрации обратимся к химии и королевству автокаталитических реакций.
Химия изучает реакции разных видов, такие как «взрывные», «пенящиеся» или «с красивыми цветами». Иногда в дело вступают особые молекулы, которые ускоряют реакции, как услужливые помощники. Их называют «катализаторами».
В некоторых, очень немногих, реакциях катализаторы производятся сами по себе. Это создает положительную обратную связь: чем больше катализаторов получается, тем быстрее и быстрее вещество пенится и/или взрывается… Но такие циклы не могут длиться вечно. Как только первоначальный запас ингредиентов на входе стремится к нулю, мы остаемся со множеством катализаторов, но катализировать теперь нечего. Реакция замедляется.
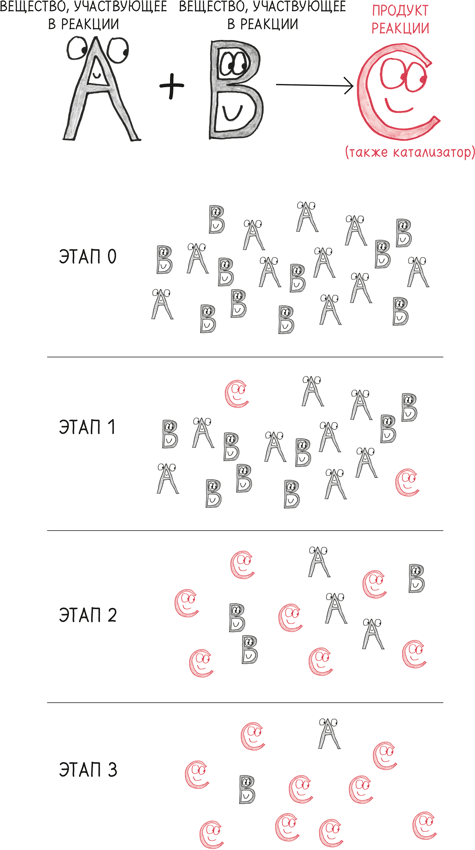
Повальные увлечения следуют той же логике. Чем больше людей ими интересуется, тем больше людей они могут привлечь. Петля обратной связи растет по экспоненте – по крайней мере, какое-то время. Но раньше или позже количество тех, кого можно привлечь к этому занятию, истощается. Вокруг множество рекрутеров, но привлекать некого. Переизбыток катализаторов, но катализировать нечего.
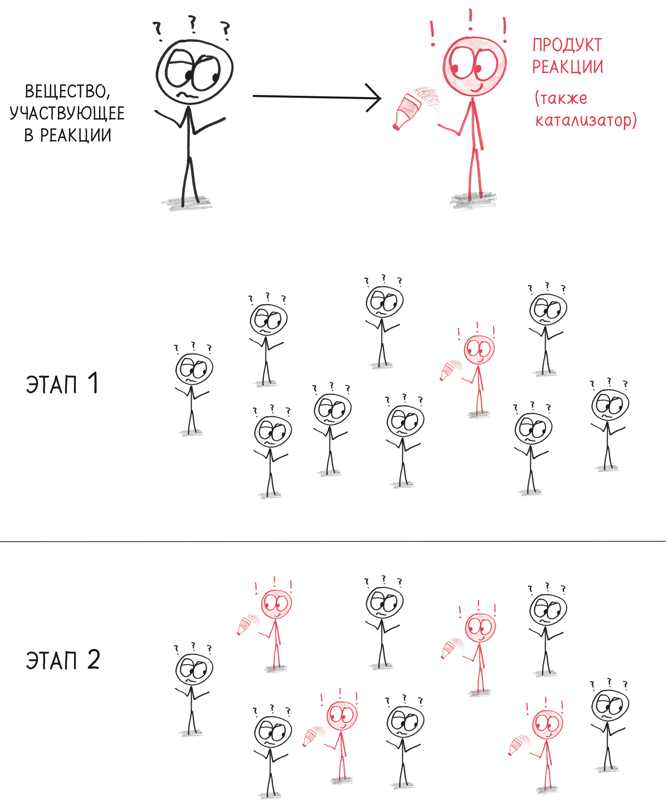
Если вам нравится пафосный химический жаргон, вы можете сказать, что вирусное массовое увлечение – это автокаталитическая реакция среди людей.
Математические модели делятся на две части. Механистические модели воплощают принципы оригинала, как модель самолета с соответствующим по размеру двигателем. Тогда как феноменологические модели имеют только поверхностное сходство, как модель самолета, которая великолепно выглядит, но летать не может.
До того как протестировать приведенную в этой главе модель, вы имеете право задать совершенно справедливый вопрос: к какому типу она принадлежит?
В Кремниевой долине сказали бы, что к механистическим моделям. Определите «коэффициент вирусности» (для количества новых людей, которых привлекает каждый последователь массового увлечения), оцените размер всего рынка, набросайте презентацию в PowerPoint, и – ба-бах! – вы готовы привлекать инвесторов.









