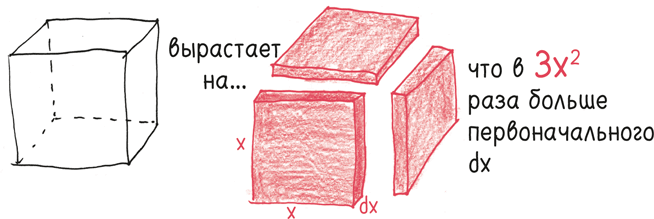
Эти последние четыре объекта – узкие стержни и претендующий на оригинальность куб – меньше самого мелкого, крошечнее крошечного. Они представляют собой практически ничто по сравнению с напоминающими листы бумаги квадратными областями. Таким образом, производная получается следующим образом: когда вы увеличиваете сторону куба, куб вырастает на три плоских квадрата, по одному на измерение.
Увидев, как визи-мат разворачивает перед ней все это, Оона внимает ему с удовольствием.
Теперь, когда она знала, что наконец может понимать все эти математические штуки, в ее крови заструилось что-то вроде пузырьков радости.
Больше не надо видеть, как Джик разочарован и задет, больше не надо слушать, как он говорит, говорит, говорит, пока она пытается понять, что, во имя Системы, все это значит. Отныне со всеми этими проблемами она может обратиться к визи-мату.
Вся эта история взята из рассказа «Алеф с нижним индексом один» (Aleph Sub One) Маргарет Сент-Клер, забытой современницы Азимова, Брэдбери и Кларка. В ее работах технологический оптимизм соединяется с социальным пессимизмом. Оона живет во времени, когда приспособления становятся все лучше и лучше, а люди остаются все теми же. «Я люблю писать об обыкновенных людях из будущего, – однажды объяснила Сент-Клер, – окруженных сложными техническими приспособлениями, порожденными супернаукой. Но эти люди, я уверена, знают о том, как вся эта техника работает, не больше, чем современный водитель осведомлен о законах термодинамики».
В этом отношении «Алеф с нижним индексом один» – выдающийся рассказ. Визи-мат, в отличие от агрегатов для уборки и приготовления пищи, одаривает Оону чем-то, что действительно имеет вес, – пониманием. Теперь она может взглянуть сквозь малопонятные формулы и увидеть стоящее за ними значение. Она может увидеть свет в конце длинного темного тоннеля лекций Джика.
Очень своеобразная точка зрения: освобождение женщины через геометрическую визуализацию.
«Битва между геометрией и алгеброй напоминает сражение между представителями различных полов, – сказал однажды математик сэр Майкл Атья. – Это навечно… Дихотомия между алгеброй как способом делать что-то с помощью формальных манипуляций и геометрией как способом мыслить на концептуальном уровне – две составляющих математики. Вопрос только в их правильном балансе».
Оона могла бы вмешаться: «В балансе? А зачем нам вообще нужна вся эта неразбериха алгебраических символов?»
Потому что геометрия имеет ограничения. Производные функций х2 и х3 нарисовать несложно, но для х4 вам придется изобразить тессеракт в четырех измерениях. Удачи вам в этом занятии. Оона попробовала это сделать на визи-мате, но без особого успеха. Она увидела «что-то вроде куба или набора кубов, от которых у нее заболели глаза». Мгновение спустя изображение исчезло, став плоским «так быстро, что Оона не была уверена, действительно ли его видела».
Именно в этот момент Оона приняла судьбоносное решение – скормить визи-мату самое ужасное, самое сложное выражение, какое она только могла придумать.
Она напряженно писала почти пять минут, обильно украшая свою работу различными dx, n-ными степенями и достаточным количеством e… Под уравнением своим круглым детским почерком Оона написала N = 5.
Когда машина затрещала и отключилась, Оона пожала плечами и ушла, занявшись хозяйством. Когда она вернулась, ее дом был поглощен «некой неестественной красноватой мутью, медленно вращающейся и напоминающей водоворот, который получается, когда вы спускаете воду из ванны». Попытка отобразить кошмарное уравнение Ооны создала уничтожающий пространство вихрь.
Для меня это выглядит правдоподобно: бессмысленные математические символы вполне способны разрушить реальность.
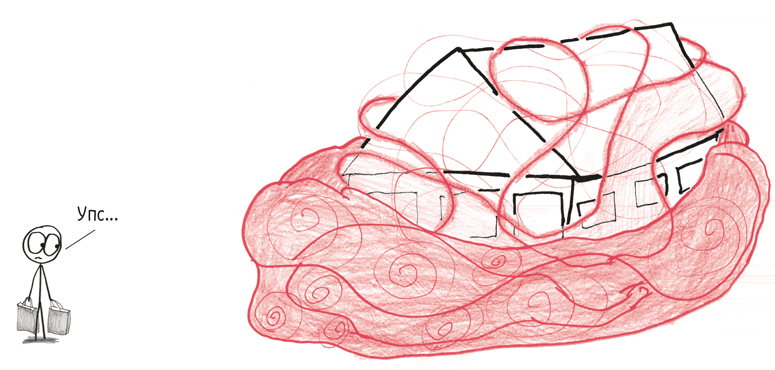
В конце концов Оона сумела спасти ситуацию, подсунув «улитке» написанную от руки записку: «Извините, я сделала ошибку. N не равна пяти. На самом деле N равна нулю (0). Вихрь получил ее записку, и «на какой-то момент казалось, что Вселенная качается на краю бездны. Затем все выглядело так, как будто нечто пожало плечами и решило утихомириться».
Возможно, не все производные могут быть визуализированы.

XI
Принцесса с городской окраины
Давным-давно, 29 или 30 столетий назад, жила-была принцесса по имени Элисса. Согласно сохранившимся текстам, ее брат Пигмалион был «тем еще парнем». Это вежливый способ рассказать о том, что он убил мужа Элиссы из желания поживиться золотом.
Прихватив с собой свои мозги, хитрость и, без сомнения, недавно возникшие проблемы с доверием, Элисса бежала через Средиземное море на побережье Африки. Она прибыла туда с большим количеством последователей, но у них не было ничего, что можно продать. Даже жульничая, Элисса сумела выторговать только «кусок земли, который она могла покрыть бычьей шкурой».

Выглядит не очень. Но Элисса была хитроумной леди. Как написано в одном из источников, она велела разрезать шкуру «на самые тонкие полосы», а затем, подойдя к прописанному в договоре с поистине вызывающей восторг ловкостью, она представила слова «участок, который можно покрыть» как «часть земли, которую можно охватить».
Такими были условия самой известной античной задачи на максимизацию. Какой участок земли вы можете отгородить с помощью некоторого количества длинных полосок кожи?

Эта загадка сегодня известна как изопериметрическая задача: приставка изо- здесь означает «тот же самый», а периметр – «подлая леди». По этимологическому совпадению периметр также означает «длина границы плоской фигуры».
Вопрос состоит в том, как можно захватить наибольшую площадь из всех возможных форм.

