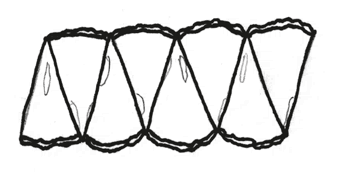
– Это почти прямоугольник, – отмечает мой оппонент. – А площадь прямоугольника найти просто. Нужно только умножить его высоту на ширину.
– Так какой же будет высота и ширина? – спрашиваю я.
– Ну, ширина – это, должно быть, половина длины окружности огурца. А высота, наверное, радиус огурца.
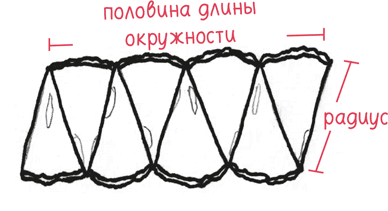
– Так задача решена?
– Не-а, – отвечает он. – На самом деле это не прямоугольник. Он неровный. Искаженный.
– Специальный термин, – объясняю я, – это «колеблющийся». Так что же нам делать?
Размышляя в этом направлении, мы берем еще один кусок огурца и рассекаем его на 24 еще более тонких ломтика. После их тщательного раскладывания получается фигура подобной формы, только слегка менее колеблющаяся, чуть менее шатающаяся. Другие гости смотрят на нас с благоговейным страхом и восхищением или, возможно, с жалостью и отвращением – я никогда не мог определить разницу.
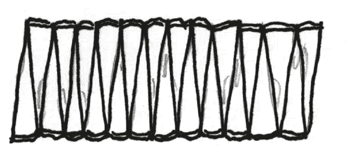
– Теперь он более прямоугольный! – говорит мой собеседник. – Но еще не совсем.
Так что мы берем еще один ломтик огурца и нарезаем его еще тоньше.

– Теперь это прямоугольник? – спрашиваю я.
Вздох:
– Нет. Он все еще колеблется по высоте и шатается по ширине. Все эти загибы здесь, пусть даже они стали микроскопическими.
– Специальный термин, – объясняю я, – это «малипусенький».
– Надо нарезать огурец на неисчислимые ломтики, каждый из которых бесконечно мал, – говорят мне. – Это единственный способ создать прямоугольник. Но… это невозможно.
Мой оппонент колеблется:
– Не так ли?
Возможно это или нет, но математик по имени Евдокс сделал это еще 24 века назад, на территории, где в наши дни находится Турция. Мы называем такой подход «методом исчерпывания» не потому, что он что-то исчерпывает, а потому, что определенное расхождение постепенно исчезает, или «исчерпывается». Это расхождение между приближением (колеблющимся прямоугольником) и тем, к чему он стремится (идеальным, свободным от колебаний прямоугольником). Проследуем по этому логическому пути до конца, и мы увидим, что площадь круга – это то же самое, что площадь прямоугольника: произведение радиуса и половины длины окружности.
Или, если вы предпочитаете уравнения:
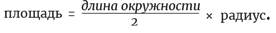
На столовой салфетке мы набросали интеграл в зачаточном виде. Рассечь проблемный объект на неисчислимые части, каждая из которых бесконечно мала; переместить их, сложить более простую совокупность и из этого перемещения сделать выводы о первоначальном объекте – эти шаги формируют шаблон, наметки интегрального исчисления.
Возможно, к этому моменту у моего собеседника кончилось вино. Вполне справедливо. Мы обмениваемся кивками и визитными карточками, чтобы больше никогда не встречаться. Предполагаю, именно для этого визитные карточки и служат – всеобщий знак, заменяющий слова «прощайте навсегда!».
Или, возможно, любопытство моего оппонента только усилилось. Он снова наполняет мой бокал, я набиваю карманы сыром, и, глубоко вдохнув, мы снова погружаемся в математику.
– Крутая формула! – говорит он. – Но это не совсем то, что я учил в школе.
– Это потому, что мы определили площадь через длину окружности, – говорю я. – А мы еще не нашли, чему равна длина окружности.
– Так как же мы это сделаем?
Вначале мы совершим небольшой экскурс в историю. Основополагающий древнекитайский трактат по математике называется «Математика в девяти книгах». Я считаю, что давать ему такое прозаическое название было просто стыдно. Другие древнекитайские математические тексты называются как-то вроде «Эссе о бассейне мечты» или «Яшмовое зеркало четырех первоэлементов». Составлявшиеся в течение нескольких веков «Девять книг» содержат в себе всё – от арифметики до геометрии и операций с матрицами, это математическая библия, обладающая неизмеримой глубиной и полнотой.
Есть только одна проблема: в ней напрочь отсутствуют объяснения. Это просто набор процедур без малейшего намека на конкретные случаи или разработку. На мой взгляд, самый худший вид учебника.
Тут на сцену выходит математик III в. Лю Хуэй. Он не был автором «Математики в девяти книгах»; он написал к ним комментарии, совсем как принц-полукровка в романе Джоан Роулинг; он был вдумчивым читателем, снабдившим примечаниями старый пыльный текст и таким образом вдохнувшим в него новую жизнь.
Оригинальная книга обходила стороной вопрос о длине окружности. Лю Хуэй был не таким человеком, чтобы не обращать на него внимания. Идя по его стопам, я набираю горсть зубочисток из фруктовой нарезки и располагаю их в виде треугольника на огуречном кружке.
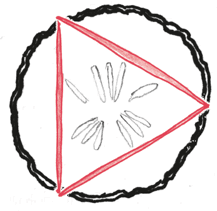
– Вот! – заявляю я. – Длина окружности!
Мой собеседник поднимает бровь.
– Каждая сторона треугольника, – объясняю я, – это
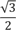 длины диаметра. Таким образом, весь периметр – это
длины диаметра. Таким образом, весь периметр – это
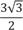 или приблизительно 2,6.
или приблизительно 2,6.
– Но это периметр треугольника, – отвечает он. – Не окружности.
– Естественно, – отвечаю я. – Кто может измерить кривую? Мы только можем приблизить ее к прямым линиям.
– Ну, если таков ваш подход, – говорит он с усмешкой, – вам лучше закончить чем-то подобным.
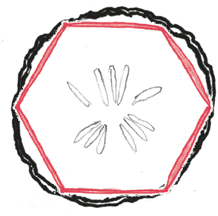







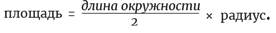

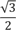 длины диаметра. Таким образом, весь периметр – это
длины диаметра. Таким образом, весь периметр – это
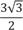 или приблизительно 2,6.
или приблизительно 2,6.