Дуглас Хофштадтер, автор книги «Гедель, Эшер, Бах: эта бесконечная гирлянда»
[63], пошел дальше. «В стремлении уничтожить парадоксы любой ценой, – пишет он, – слишком много внимания уделяют плоской последовательности и логичности и слишком мало тому причудливому и замысловатому, что придает вкус жизни и математике». Парадоксы прекрасны сами по себе, а работы Эшера хороши и без краски. Или, в данном случае, с бесконечным окрашиванием.
XХVIII
Сцены из невозможности
Мое первое прикосновение к Неберущемуся Интегралу состоялось весной, когда я учился в десятом классе.
Группа выпускников собралась в коридоре. Они были вооружены ручками и покрывали плакат закорючками, подписями и выдернутыми из контекста цитатами высказываний нашего учителя физики мистера Риахи. Это был обширный коллаж, полный шуток, которых я не понимал, шуток, которые я понимал наполовину, и шуток, которые мне очень хотелось понять.
Среди всего этого хаоса я заметил необычную мешанину символов:
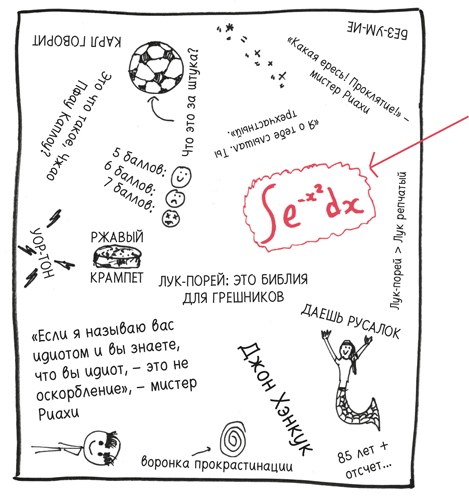
Я указал на нее:
– Что это?
– Это интеграл e в степени – х в квадрате, – объяснил Дэвид, не прояснив ничего.
– Так в чем же шутка? – спросил я.
– ШУТКА В ТОМ, ЧТО ОН НЕБЕРУЩИЙСЯ, – ответила Эбби, которая всегда разговаривала, словно писала большими буквами.
– А-а-а-а-а… его проверяли? Никто не смог его решить?
Они захихикали.
– АХ, НЕДОУЧКА БЕН, ТРЕТИЙ ИЗ ТРЕХ, – обратилась ко мне Эбби (так оно и было: Бен Копанс и Бен Миллер стояли передо мной в алфавитном списке). – КАКОЙ ТЫ НЕВИННЫЙ И ТРОГАТЕЛЬНЫЙ!
– Как бы то ни было, если под проверкой ты имеешь в виду «когда-либо во Вселенной», – задумчиво сказал Барт, – то да. Его проверяли. И никто не смог его решить.
– То есть это как… делить на ноль? – спросил я.
– Скорее как делать из круга квадрат, – ответил Дэвид.
– ЭТО КАК ДОЖДЬ В ДЕНЬ ТВОЕЙ СВАДЬБЫ! – уточнила Эбби. – КАК ДЕСЯТЬ ТЫСЯЧ ЛОЖЕК, КОГДА ВСЕ, ЧТО ТЕБЕ НУЖНО, – ЭТО НОЖ!
Эбби была права. Если вернуться в детство математического анализа, Иоганн Бернулли писал об угрозе неберущихся интегралов. «Иногда мы не в состоянии сказать с полной уверенностью, можем ли найти интеграл заданной величины». В XIX в. математик Жозеф Лиувилль сказал об этом с определенностью: некоторые интегралы взять нельзя. Например,
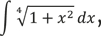 или ∫ ln (lnx) dx, или
или ∫ ln (lnx) dx, или
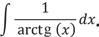 У этих интегралов нет чистых решений, точнее говоря, они «неразрешимы в элементарных функциях». Соберите все синусы, все косинусы, все логарифмы и кубические корни, какие вам захочется, но ни одна из стандартных алгебраических «отмычек» никогда не подойдет к формуле. Это замок без ключа, загадка без ответа, жесткий стейк в мире 10 000 ложек.
У этих интегралов нет чистых решений, точнее говоря, они «неразрешимы в элементарных функциях». Соберите все синусы, все косинусы, все логарифмы и кубические корни, какие вам захочется, но ни одна из стандартных алгебраических «отмычек» никогда не подойдет к формуле. Это замок без ключа, загадка без ответа, жесткий стейк в мире 10 000 ложек.
Я смотрел на символы. Большая загогулина не значила для меня ничего, пока еще нет. «Мы начнем матан через девять месяцев, – заметил ранее мой друг Роз, – и ты знаешь, что это означает: кто-то залетел от моего графического калькулятора». Шутку Роза я понял, но шутка выпускников ускользнула от моего ума.
Перенесемся на восемь лет вперед.
Моя первая работа в качестве преподавателя заставила меня задуматься о торговле подержанными автомобилями на окраине китайского квартала Окленда. Однажды на третий год преподавания я показал своим ученикам продвинутого курса математического анализа неберущийся интеграл: ∫ e−x2 dx. В витиеватых и напыщенных выражениях я разъяснил его нерешаемость.
– Спойлер! – выкрикнула Адриана.
Несколько студентов покачали головами.
Но Бетсайда задала мне провокационный вопрос:
– Так у него нет области под кривой?
Ага, хорошая задачка! Думаю, никто не удивился, что я был небрежен и понятия не имел, как ответить на этот вопрос. Выяснилось, что у функции e−x2 есть чрезвычайно красивый график.
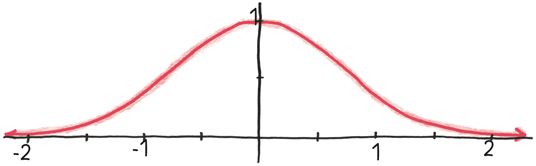
Если вы возьмете конкретную ограниченную область – скажем, от 0 до 1, или от 0,9 до 1,3, или от –1,5 до 0,5, то в самом деле найдете ответ.
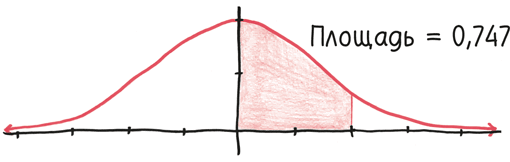
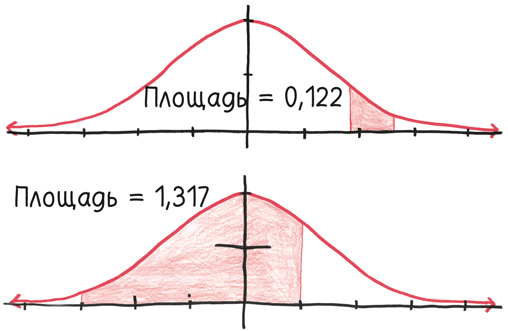
Тогда почему интеграл «неберущийся»? Потому что нет хорошей формулы для определения этой площади. Наша волшебная палочка – фундаментальная теорема математического анализа, которая вычисляет интегралы, беря антипроизводные, – здесь оказывается просто бесполезным прутиком. Машите ею хоть сотню лет: никакого магического ответа так и не появится.
– Мой графический калькулятор может это сделать, – сказал Ю Ханг. – То есть, если судить по вашим словам, он умнее всех математиков в мире.
– Ну… – я закашлялся. – Он определенно быстрее аппроксимирует интегралы через суммы Римана.
Самое лучшее, что мы можем сделать с такими функциями, – это аппроксимация. Мой тон выдавал мои предрассудки. Аппроксимация – это не настоящее решение. Она приблизительная. Второразрядная. Не считается.
– А вы уверены? – подзуживал Ю Ханг. – Этот калькулятор, кажется, умнее меня.
Когда урок закончился, я выскользнул из класса через заднюю дверь, которая в стиле Нарнии вела в кабинет статистики. Ее я преподавал первый год и все время спотыкался. Все мои инстинкты были чисто математическими, все доказательства и абстракции для статистики не подходили. Я чувствовал себя так, как будто перепутал виды спорта, словно учу детей сбивать подпрыгивающим теннисным мячиком кегли.





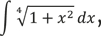 или ∫ ln (lnx) dx, или
или ∫ ln (lnx) dx, или
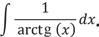 У этих интегралов нет чистых решений, точнее говоря, они «неразрешимы в элементарных функциях». Соберите все синусы, все косинусы, все логарифмы и кубические корни, какие вам захочется, но ни одна из стандартных алгебраических «отмычек» никогда не подойдет к формуле. Это замок без ключа, загадка без ответа, жесткий стейк в мире 10 000 ложек.
У этих интегралов нет чистых решений, точнее говоря, они «неразрешимы в элементарных функциях». Соберите все синусы, все косинусы, все логарифмы и кубические корни, какие вам захочется, но ни одна из стандартных алгебраических «отмычек» никогда не подойдет к формуле. Это замок без ключа, загадка без ответа, жесткий стейк в мире 10 000 ложек.

